Question

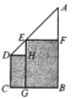
【题目】如图，在四边形中，，，，，点是边上一点，过点分别作与的垂线，过点作的垂线，得到矩形和矩形，则这两个矩形的面积之和的最大值是_________．

Answer 1

【答案】

【解析】

延长DH交AB于点I，则DI⊥AB，利用矩形和等腰直角三角形的性质，求出CD的长度，然后求出S与x的关系式，利用二次函数的性质，即可得到答案.

解：根据题意，，

延长DH交AB于点I，则DI⊥AB，

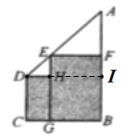
∴四边形BCDI是矩形，

∴DI=BC=3，CD=BI，

由，DI⊥AB，

∴△ADI是等腰直角三角形，

∴AI=DI=3，

∴CD=BI=，

∵△AEF是等腰直角三角形，

∴EF=AF；

设EF=AF=x，则FI=3-x，

∴这两个矩形的面积之和为：，

即；

∵，

∴当时，这两个矩形的面积之和有最大值，最大值为；

故答案为：.