题目内容
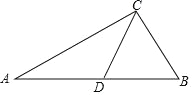
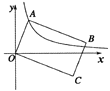
【题目】如图,![]() 是
是![]() 的外接圆,且
的外接圆,且![]() ,延长
,延长![]() 至点
至点![]() ,使得
,使得![]() ,点
,点![]() 是
是![]() 上的一个动点,连结
上的一个动点,连结![]() ,
,![]() ,
,![]() .
.
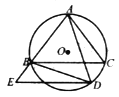
(1)当![]() 时,求证:
时,求证:![]() ;
;
(2)若![]() ,则:
,则:
①求![]() 的半径;
的半径;
②当![]() 为直角三角形时,求
为直角三角形时,求![]() 的长.
的长.
【答案】(1)证明见解析;(2)①![]() ;②
;②![]() 或
或![]() .
.
【解析】
(1)根据平行线的性质得到∠ABC=∠E,根据圆周角定理得到∠ADB=∠ACB,等量代换证明结论;
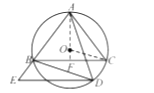
(2)①连接AO并延长交BC于F,连接OC,根据垂径定理得到AF⊥BC,根据等腰三角形的性质求出CF,根据勾股定理求出AF,根据勾股定理列式计算即可;
②分∠ABD=90°、∠BAD=90°两种情况,根据勾股定理计算,得到答案.
解:(1)∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() .
.
(2)①连接![]() 并延长交
并延长交![]() 于点
于点![]() ,连接
,连接![]() .
.
∵![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
在![]() 中,
中,![]() ,由勾股定理得:
,由勾股定理得:![]() ,
,
设半径为![]() ,则
,则![]() ,
,
由勾股定理,得:![]() ,
,
解得:![]() .
.
②当![]() 运动到
运动到![]() 过圆
过圆![]() 时,
时,![]() ,
,
∴AD=![]() ,
,
∴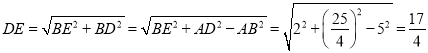 .
.
当![]() 运动到
运动到![]() 过圆
过圆![]() 时,
时,![]() ,
,
∴BD=![]() ,
,
∴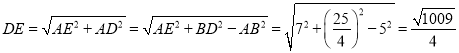 .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目