题目内容
如图，⊙O的半径为2，点P是半径OA上的一个动点，过点P作直线MN且∠APN=60°，过点A的切线AB交MN于点B．设OP=x，△PAB的面积为 y，则下列图象中，
能表示y与x的函数关系的图象大致是（ ）
D
【解析】
试题分析：由题意知OA=2，OP=x，因此可得AP=2-x，再由切线的性质可知OA⊥AB，根据∠APB=60°，可根据锐角三角函数可知tan60°=
，即
，因此AB=
，所以
，即y=
，由此可得其对称轴为x=2，与y轴的交点为（0，
）．
故选D
考点：锐角三角函数，切线的性质
练习册系列答案
相关题目
B．
C．
D．
甲、乙两种水稻试验品种连续5年的平均单位面积产量如下（单位：吨/公顷）：
品种 | 第1年 | 第2年 | 第3年 | 第4年 | 第5年 |
甲 | 9.8 | 9.9 | 10.1 | 10 | 10.2 |
乙 | 9.4 | 10.3 | 10.8 | 9.7 | 9.8 |
为使水稻品种的产量比较稳定，根据题中所给的数据，你选择哪种水稻品种？请说明理由.
，
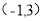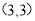是二次函数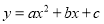
图象上的两点，则此二次函数的对称轴是（ ）
；
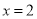
的值：
．