题目内容
17. 如图,在△ABC中,∠ACB=90°,∠A=30°,BE平分∠ABC,DE⊥AB于D,如果AC=4$\sqrt{3}$cm,那么△ADE的周长等于4$\sqrt{3}$+4cm.
如图,在△ABC中,∠ACB=90°,∠A=30°,BE平分∠ABC,DE⊥AB于D,如果AC=4$\sqrt{3}$cm,那么△ADE的周长等于4$\sqrt{3}$+4cm.
分析 由BE为角平分线,且DE垂直于BA,EC垂直于BC,利用角平分线性质得到DE=CE,则AE+DE+AD=(AE+CE)+AD=AC+AD,故可得出结论.
解答 解:∵∠ACB=90°,
∴EC⊥BC,
又∵BE平分∠ABC,DE⊥AB,
∴DE=CE,∠DBE=∠CBE,
∵∠A=30°
∴AB=2BC,∠DBE=30°,
又∵AC=4$\sqrt{3}$cm,
∴BC=4cm,AB=8cm,
∴AD=BD=4cm,
∴AE+DE=AE+CE=AC=4$\sqrt{3}$cm.
∴AE+DE+AD=(AE+CE)+AD=AC+AD=(4$\sqrt{3}$+4)cm.
故答案为4$\sqrt{3}$+4.
点评 本题考查了角平分线的性质,熟知角的平分线上的点到角的两边的距离相等是解答此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
7. 有理数在数轴上的位置如图所示,则|m-n|的值为( )
有理数在数轴上的位置如图所示,则|m-n|的值为( )
 有理数在数轴上的位置如图所示,则|m-n|的值为( )
有理数在数轴上的位置如图所示,则|m-n|的值为( )| A. | n-m | B. | m-n | C. | m+n | D. | -m-n |
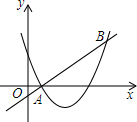 如图,直线y=x+m和抛物线y=x2+bx+c都经过点A(1,0),B(3,2),不等式x2+bx+c<x+m的解集为1<x<3.
如图,直线y=x+m和抛物线y=x2+bx+c都经过点A(1,0),B(3,2),不等式x2+bx+c<x+m的解集为1<x<3.