题目内容
已知抛物线 经过
经过 ,
, ,
, 。
。
(1)求此抛物线的解析式;
(2)求出顶点 的坐标,连接
的坐标,连接 ,求证△
,求证△ ∽△
∽△ ;
;
(3)在直线 上方的抛物线上是否存在一点M,使S△
上方的抛物线上是否存在一点M,使S△ 最大,求出M的坐标;
最大,求出M的坐标;
 经过
经过 ,
, ,
, 。
。(1)求此抛物线的解析式;
(2)求出顶点
 的坐标,连接
的坐标,连接 ,求证△
,求证△ ∽△
∽△ ;
;(3)在直线
 上方的抛物线上是否存在一点M,使S△
上方的抛物线上是否存在一点M,使S△ 最大,求出M的坐标;
最大,求出M的坐标;(1) ;(2)先配方得到顶点
;(2)先配方得到顶点 的坐标,再根据勾股定理求得BC、CD、BD、OC、OA、AC的长,根据相似三角形的判定方法即可证得结论;(3)M(
的坐标,再根据勾股定理求得BC、CD、BD、OC、OA、AC的长,根据相似三角形的判定方法即可证得结论;(3)M( ,
, )
)
 ;(2)先配方得到顶点
;(2)先配方得到顶点 的坐标,再根据勾股定理求得BC、CD、BD、OC、OA、AC的长,根据相似三角形的判定方法即可证得结论;(3)M(
的坐标,再根据勾股定理求得BC、CD、BD、OC、OA、AC的长,根据相似三角形的判定方法即可证得结论;(3)M( ,
, )
)试题分析:(1)根据待定系数法即可求得结果;
(2)先配方得到顶点
 的坐标,再根据勾股定理求得BC、CD、BD、OC、OA、AC的长,根据相似三角形的判定方法即可证得结论;
的坐标,再根据勾股定理求得BC、CD、BD、OC、OA、AC的长,根据相似三角形的判定方法即可证得结论;(3)设M(
 ),根据三角形的面积公式表示出△BCM的面积,再根据二次函数的性质即可求得结果.
),根据三角形的面积公式表示出△BCM的面积,再根据二次函数的性质即可求得结果.(1)将
 ,
, ,
, 代入抛物线
代入抛物线 中,
中,得
 ,解得
,解得 ,
,∴抛物线的解析式为
 ;
;(2)∵

∴顶点
 的坐标为(1,4)
的坐标为(1,4)∴
 ,
, ,
, ,
, ,
, ,
,
∵

∴△
 ∽△
∽△ ;
;(3)设M(
 )
)S△
 =
= =
= =
=
当
 时,S△
时,S△ 最大,此时
最大,此时 ,
,∴M(
 ,
, ).
).点评:解答本题的关键是读懂题意,找到等量关系,正确列出函数关系式,同时熟练掌握二次函数的最大值的求法.

练习册系列答案
相关题目

 ≠0的图像经过点(3,5)、(2,8)、(0,8).
≠0的图像经过点(3,5)、(2,8)、(0,8). ≠0,
≠0, ≠0,且满足
≠0,且满足 ≠0,1,则我们称抛物线
≠0,1,则我们称抛物线 互为“友好抛物线”,请写出当
互为“友好抛物线”,请写出当 时第(1)小题中的抛物线的友好抛物线,并求出这友好抛物线的顶点坐标.
时第(1)小题中的抛物线的友好抛物线,并求出这友好抛物线的顶点坐标.
 的对称轴为
的对称轴为 )
) 天(
天( 且
且
 (元)与
(元)与 ,△DCQ的面积为y1平方厘米,△PCQ的面积为y2平方厘米.
,△DCQ的面积为y1平方厘米,△PCQ的面积为y2平方厘米.

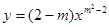 是二次函数,求m的值
是二次函数,求m的值 ,当自变量
,当自变量 取两个不同的值
取两个不同的值 时函数值相等,则当自变量
时函数值相等,则当自变量 时函数值与( )
时函数值与( ) 时的函数值相等
时的函数值相等  时的函数值相等
时的函数值相等 时的函数值相等
时的函数值相等  时的函数值相等
时的函数值相等 的图象如图所示,当y<0时,自变量 x的取值范围为 ( )
的图象如图所示,当y<0时,自变量 x的取值范围为 ( )