题目内容
已知,在平行四边形OABC中,OA=5,AB=4,∠OCA=90°,动点P从O点出发沿射线OA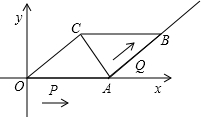 方向以每秒2个单位的速度移动,同时动点Q从A点出发沿射线AB方向以每秒1个单位的速度移动.设移动的时间为t秒.
方向以每秒2个单位的速度移动,同时动点Q从A点出发沿射线AB方向以每秒1个单位的速度移动.设移动的时间为t秒.(1)求直线AC的解析式;
(2)试求出当t为何值时,△OAC与△PAQ相似.
分析:(1)要求直线AC的解析式,需要求出点A、点C的坐标,可以利用等积法求得C点的纵坐标,利用勾股定理求得横坐标,利用两点式求得直线的解析式;
(2)对于相似要分情况进行讨论,根据对应线段成比例可求得t的数值.
(2)对于相似要分情况进行讨论,根据对应线段成比例可求得t的数值.
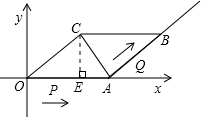
解答:解:(1)过点C作CE⊥OA,垂足为E,
在Rt△OCA中,AC=
=3,
∴5×CE=3×4,
∴CE=
,
在Rt△OCE中,OE=
=
,
∴C(
,
),A(5,0),
 ∴y=-
∴y=-
x+
;
(2)当0≤t≤2.5时,P在OA上,若∠OAQ=90°时,
故此时△OAC与△PAQ不可能相似.
当t>2.5时,
①若∠APQ=90°,则△APQ∽△OCA,
故
=
=
,
∴
=
,
∴t=
,
∵t>2.5,
∴t=
符合条件.
②若∠AQP=90°,则△APQ∽△OAC,
故
=
=
,
∴
=
,
∴t=
,
∵t>2.5,
∴t=
符合条件.
综上可知,当t=
或
时,△OAC与△APQ相似.
在Rt△OCA中,AC=
| 52-42 |
∴5×CE=3×4,
∴CE=
| 12 |
| 5 |
在Rt△OCE中,OE=
42-(
|
| 16 |
| 5 |
∴C(
| 16 |
| 5 |
| 12 |
| 5 |
 ∴y=-
∴y=-| 4 |
| 3 |
| 20 |
| 3 |
(2)当0≤t≤2.5时,P在OA上,若∠OAQ=90°时,
故此时△OAC与△PAQ不可能相似.
当t>2.5时,
①若∠APQ=90°,则△APQ∽△OCA,
故
| AQ |
| AP |
| OA |
| OC |
| 5 |
| 4 |
∴
| t |
| 2t-5 |
| 5 |
| 4 |
∴t=
| 25 |
| 6 |
∵t>2.5,
∴t=
| 25 |
| 6 |
②若∠AQP=90°,则△APQ∽△OAC,
故
| AQ |
| AP |
| OC |
| OA |
| 4 |
| 5 |
∴
| t |
| 2t-5 |
| 4 |
| 5 |
∴t=
| 20 |
| 3 |
∵t>2.5,
∴t=
| 20 |
| 3 |
综上可知,当t=
| 25 |
| 6 |
| 20 |
| 3 |
点评:本题考查了相似三角形的判定与性质、平行四边形的性质及直讨论线与圆的位置关系;在解决圆的问题时要注意勾股定理的应用,要注意对问题进行分类讨论.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
 已知:在平行四边形ABCD中,对角线AC、BD相交于点O,M、N、P、Q分别是OA、OB、OC、OD的中点.
已知:在平行四边形ABCD中,对角线AC、BD相交于点O,M、N、P、Q分别是OA、OB、OC、OD的中点. 以每秒2个单位的速度移动,同时动点Q从A点出发沿射线AB方向以每秒1个单位的速度移动.设移动的时间为t秒.
以每秒2个单位的速度移动,同时动点Q从A点出发沿射线AB方向以每秒1个单位的速度移动.设移动的时间为t秒. 如图,已知:在平行四边形ABCD中,AB=4cm,AD=7cm,∠ABC的平分线交AD于点E,交CD的延长线于点F,求DF的长.
如图,已知:在平行四边形ABCD中,AB=4cm,AD=7cm,∠ABC的平分线交AD于点E,交CD的延长线于点F,求DF的长.