题目内容
 已知:在平行四边形ABCD中,对角线AC、BD相交于点O,M、N、P、Q分别是OA、OB、OC、OD的中点.
已知:在平行四边形ABCD中,对角线AC、BD相交于点O,M、N、P、Q分别是OA、OB、OC、OD的中点.求证:四边形MNPQ是平行四边形.
分析:运用中位线定理和四边形ABCD为平行四边形,可得MN∥PQ,MN=PQ,再根据平行四边形的判定可得出结论.
解答:证明:∵M、N、P、Q分别是OA、OB、OC、OD的中点,
∴MN∥AB,MN=
AB;PQ∥CD,PQ=
CD.
又∵ABCD是平行四边形,
∴AB∥CD,AB=CD.
∴MN∥PQ,MN=PQ.
∴四边形PQMN是平行四边形.
∴MN∥AB,MN=
| 1 |
| 2 |
| 1 |
| 2 |
又∵ABCD是平行四边形,
∴AB∥CD,AB=CD.
∴MN∥PQ,MN=PQ.
∴四边形PQMN是平行四边形.
点评:本题考查了平行四边形的判定和三角形的中位线定理,三角形的中位线的性质定理,为证明线段相等和平行提供了依据.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
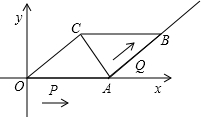 方向以每秒2个单位的速度移动,同时动点Q从A点出发沿射线AB方向以每秒1个单位的速度移动.设移动的时间为t秒.
方向以每秒2个单位的速度移动,同时动点Q从A点出发沿射线AB方向以每秒1个单位的速度移动.设移动的时间为t秒. 以每秒2个单位的速度移动,同时动点Q从A点出发沿射线AB方向以每秒1个单位的速度移动.设移动的时间为t秒.
以每秒2个单位的速度移动,同时动点Q从A点出发沿射线AB方向以每秒1个单位的速度移动.设移动的时间为t秒. 如图,已知:在平行四边形ABCD中,AB=4cm,AD=7cm,∠ABC的平分线交AD于点E,交CD的延长线于点F,求DF的长.
如图,已知:在平行四边形ABCD中,AB=4cm,AD=7cm,∠ABC的平分线交AD于点E,交CD的延长线于点F,求DF的长.