题目内容

已知：在平行四边形ABCD中，设
AB
=
a
，
AD
=
b
，那么
CA
=
 
（用向量
a
、
b
的式子表示）．
分析：由在平行四边形ABCD中，可得
BC
=
AD
=
b
，即可得
BA
=-
a
，
CB
=-
b
，又由
CA
=
CB
+
BA
，即可求得答案．
解答：精英家教网解：∵四边形ABCD是平行四边形，
∴AD∥BC，AD=BC，
∴
BC
=
AD
=
b
，
∵
AB
=
a
，
∴
BA
=-
a
，
CB
=-
b
，
∴
CA
=
CB
+
BA
=-
b
-
a
．
故答案为：-
b
-
a
．
点评：此题考查了平面向量的知识与平行四边形的性质．此题难度不大，注意数形结合思想的应用．
练习册系列答案
相关题目
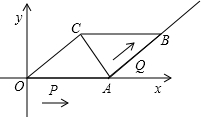已知，在平行四边形OABC中，OA=5，AB=4，∠OCA=90°，动点P从O点出发沿射线OA精英家教网方向以每秒2个单位的速度移动，同时动点Q从A点出发沿射线AB方向以每秒1个单位的速度移动．设移动的时间为t秒．
（1）求直线AC的解析式；  
（2）试求出当t为何值时，△OAC与△PAQ相似．
精英家教网已知：在平行四边形ABCD中，对角线AC、BD相交于点O，M、N、P、Q分别是OA、OB、OC、OD的中点．
求证：四边形MNPQ是平行四边形．
已知，在平行四边形OABC中，OA=5，AB=4，∠OCA=90°，动点P从O点出发沿射线OA方向精英家教网以每秒2个单位的速度移动，同时动点Q从A点出发沿射线AB方向以每秒1个单位的速度移动．设移动的时间为t秒．
（1）求直线AC的解析式；
（2）试求出当t为何值时，△OAC与△PAQ相似？
（3）若⊙P的半径为
8
5
，⊙Q的半径为
3
2
；当⊙P与对角线AC相切时，判断⊙Q与直线AC、BC的位置关系，并求出Q点坐标．
如图，已知：在平行四边形ABCD中，AB=4cm，AD=7cm，∠ABC的平分线交AD于点E，交CD的延长线于点F，求DF的长．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网