题目内容
 如图所示,点P在圆O上,将圆心角∠AOC绕点O按逆时针旋转到∠BOD,旋转角为α(0°<α<180°).若∠AOC=β(0°<β<180°),则∠P的度数为(用α和β表示)
如图所示,点P在圆O上,将圆心角∠AOC绕点O按逆时针旋转到∠BOD,旋转角为α(0°<α<180°).若∠AOC=β(0°<β<180°),则∠P的度数为(用α和β表示)
- A.

- B.

- C.β-α
- D.α+β
A
分析:根据圆心角∠AOC绕点O按逆时针旋转到∠BOD,旋转角为α(0°<α<180°)可知∠AOB=α,再由∠AOC=β可求出∠COB的度数,根据圆周角定理即可求出∠P的度数.
解答:∵圆心角∠AOC绕点O按逆时针旋转到∠BOD,旋转角为α(0°<α<180°),
∴∠AOB=α,
∵∠AOC=β,
∴∠COB=α-β,
∴∠P= =
=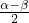 .
.
故选A.
点评:本题考查的是圆周角定理及图形的旋转,解答此题的关键是弄清旋转角即为∠AOB的度数.
分析:根据圆心角∠AOC绕点O按逆时针旋转到∠BOD,旋转角为α(0°<α<180°)可知∠AOB=α,再由∠AOC=β可求出∠COB的度数,根据圆周角定理即可求出∠P的度数.
解答:∵圆心角∠AOC绕点O按逆时针旋转到∠BOD,旋转角为α(0°<α<180°),
∴∠AOB=α,
∵∠AOC=β,
∴∠COB=α-β,
∴∠P=
 =
=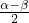 .
.故选A.
点评:本题考查的是圆周角定理及图形的旋转,解答此题的关键是弄清旋转角即为∠AOB的度数.

练习册系列答案
相关题目
 如图所示,点P在圆O上,将圆心角∠AOC绕点O按逆时针旋转到∠BOD,旋转角为α(0°<α<180°).若∠AOC=β(0°<β<180°),则∠P的度数为(用α和β表示)( )
如图所示,点P在圆O上,将圆心角∠AOC绕点O按逆时针旋转到∠BOD,旋转角为α(0°<α<180°).若∠AOC=β(0°<β<180°),则∠P的度数为(用α和β表示)( )A、
| ||
B、
| ||
| C、β-α | ||
| D、α+β |




 (B)
(B) (C)
(C) (D)α+β
(D)α+β



