Question

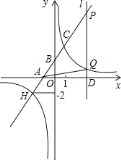
【题目】如图，点P，Q是直线y=x+2上的两点，点P在点Q的左侧，且满足OP=OQ，OP⊥OQ，则点Q的坐标是______.

Answer 1

【答案】（，）.

【解析】

分别过点P、Q作x轴的垂线于点M、N，证明△PMO≌△ONQ（AAS），则PM=ON，OM=QN，设点P（m，m+2），则点Q（m+2，－m），将点Q代入y=x+2求出m即可得解．

解：分别过点P、Q作x轴的垂线于点M、N，

∵OP⊥OQ，

∴∠POM+∠QON=90°，而∠QON+∠OQN=90°，
∴∠OQN=∠MOP，

∵OP=OQ，∠PMO=∠ONQ=90°，
∴△PMO≌△ONQ（AAS），
∴PM=ON，OM=QN，
设点P（m，m+2），则点Q（m+2，－m），
将点Q的坐标代入y=x+2得：－m=（m+2）+2，
解得：m=，

∴m+2=，
故点Q（，），
故答案为：（，）.