Question

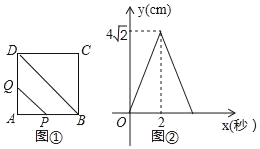
【题目】如图①，在边长为4cm的正方形ABCD中，点P以每秒2cm的速度从点A出发，沿AB→BC的路径运动，到点C停止．过点P作PQ∥BD，PQ与边AD（或边CD）交于点Q，PQ的长度y（cm）与点P的运动时间x（秒）的函数图象如图②所示．当点P运动2.5秒时，PQ的长度是________cm．

Answer 1

【答案】

【解析】

根据运动速度乘以时间，可得P点运动的距离，根据线段的和差，可得CP的长，根据勾股定理，即可求出答案．

解：由图②可知点P运动2.5秒，P在BC上，

由PQ∥BD，得Q在CD上，且∠CQP=∠CDB=45°，即CQ=CP，

CP=AB+BC-2.5×2=8-5=3cm，

CQ=CP=3cm，

由勾股定理得：PQ==cm．

故答案为：．