题目内容
 如图,是一块四边形草坪,∠B=90°,AB=24m,BC=7m,CD=15m,AD=20m,求草坪面积.
如图,是一块四边形草坪,∠B=90°,AB=24m,BC=7m,CD=15m,AD=20m,求草坪面积.考点:勾股定理的应用
专题:
分析:连接AC,先根据勾股定理求出AC的长,再求出AD的长,由S四边形ABCD=S△ABC+S△ADC即可得出结论.
解答: 解:连接AC,
解:连接AC,
∵∠B=90°,AB=24m,BC=7m,
∴AC2=AB2+BC2=242+72=625,
∴AC=25(m).
又∵CD=15m,AD=20m,152+202=252,即AD2+DC2=AC2,
∴△ACD是直角三角形,
∴S四边形ABCD=S△ABC+S△ADC
=
•AB•BC+
•AD•DC
=234(m2).
 解:连接AC,
解:连接AC,∵∠B=90°,AB=24m,BC=7m,
∴AC2=AB2+BC2=242+72=625,
∴AC=25(m).
又∵CD=15m,AD=20m,152+202=252,即AD2+DC2=AC2,
∴△ACD是直角三角形,
∴S四边形ABCD=S△ABC+S△ADC
=
| 1 |
| 2 |
| 1 |
| 2 |
=234(m2).
点评:本题考查的是勾股定理的应用,熟知勾股定理的应用是解答此题的关键.

练习册系列答案
相关题目
 如图,P是∠BAC的平分线AD上一点,PE⊥AB于E,PF⊥AC于F,若AE=4,则AF=( )
如图,P是∠BAC的平分线AD上一点,PE⊥AB于E,PF⊥AC于F,若AE=4,则AF=( )| A、1 | B、2 | C、4 | D、8 |
某服装店新开张,第一天销售服装a件,第二天的销售件数是第一天销售件数的3倍还多10件,则第二天销售了( )
| A、(a+10)件 |
| B、(3a+13)件 |
| C、(10a+3)件 |
| D、(3a+10)件 |
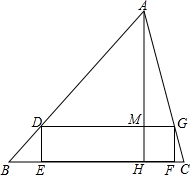 如图,一块三角形土地的底边BC=100m,高AH=80m.某单位要沿着底边BC修一座底面是矩形DEFG的大楼,设矩形DEFG的一边DE=x(m).当DE为多少时,大楼底面的面积最大?最大值是多少?
如图,一块三角形土地的底边BC=100m,高AH=80m.某单位要沿着底边BC修一座底面是矩形DEFG的大楼,设矩形DEFG的一边DE=x(m).当DE为多少时,大楼底面的面积最大?最大值是多少?