题目内容
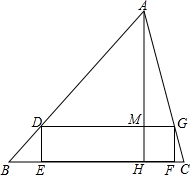 如图,一块三角形土地的底边BC=100m,高AH=80m.某单位要沿着底边BC修一座底面是矩形DEFG的大楼,设矩形DEFG的一边DE=x(m).当DE为多少时,大楼底面的面积最大?最大值是多少?
如图,一块三角形土地的底边BC=100m,高AH=80m.某单位要沿着底边BC修一座底面是矩形DEFG的大楼,设矩形DEFG的一边DE=x(m).当DE为多少时,大楼底面的面积最大?最大值是多少?考点:相似三角形的应用,二次函数的最值
专题:
分析:两三角形相似,对应高之比等于相似比.利用此性质即可解答.
解答:解:设DE的长为x,矩形DEFG面积为y,
∵矩形DEFG的边EF在△ABC的边BC上,
∴DG∥BC,(1分)
∴△ADG∽△ABC(2分)
∵AH⊥BC,
∴AM⊥DG
∴
=
,
∴
=
,(2分)
∴DG=100-
x,(1分)
∴y=-
x2+100x=-
(x-40)2+2000,
∴当DE的长为40米时,有最大面积,最大面积为2000平方米.
∵矩形DEFG的边EF在△ABC的边BC上,
∴DG∥BC,(1分)
∴△ADG∽△ABC(2分)
∵AH⊥BC,
∴AM⊥DG
∴
| AM |
| AH |
| DG |
| BC |
∴
| 80-x |
| 80 |
| DG |
| 100 |
∴DG=100-
| 5 |
| 4 |
∴y=-
| 5 |
| 4 |
| 5 |
| 4 |
∴当DE的长为40米时,有最大面积,最大面积为2000平方米.
点评:考查了相似三角形的应用,本题中求得x的值使得xy有最大值是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,是一块四边形草坪,∠B=90°,AB=24m,BC=7m,CD=15m,AD=20m,求草坪面积.
如图,是一块四边形草坪,∠B=90°,AB=24m,BC=7m,CD=15m,AD=20m,求草坪面积. 一艘海轮以30海里/时的速度由西向东航行,途中接到台风警报,台风中心正以60海里/时的速度由南向北移动,距台风中心30
一艘海轮以30海里/时的速度由西向东航行,途中接到台风警报,台风中心正以60海里/时的速度由南向北移动,距台风中心30