题目内容
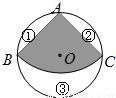
从一个直径是2的圆形铁皮中剪下一个圆心角为90°的扇形．求这个扇形半径AB的长度、扇形的弧长及面积（结果保留π）．
分析：连接BC，根据90度的圆周角所对的弦是直径可知BC是直径且AB=AC，再利用勾股定理即可求得AB的长，分别把圆心角是90度，半径是2代入弧长公式和扇形的面积公式即可求得扇形的弧长及面积．
解答：
解：连接BC，
∵∠A=90°
∴BC是直径，BC=2
在Rt△ABC中，由勾股定理求得：AB=AC=
，
∴l=
=
∴S=
=
π．
解：连接BC，∵∠A=90°
∴BC是直径，BC=2
在Rt△ABC中，由勾股定理求得：AB=AC=
| 2 |
∴l=
| nπR |
| 180 |
| ||
| 2 |
∴S=
| πnR2 |
| 360 |
| 1 |
| 2 |
点评：要知道圆的一般性质（90度的圆周角所对的弦是直径）．要牢记扇形的面积公式和弧长公式．面积公式：S=
；弧长公式：C=
．
| nπr2 |
| 360 |
| nπr |
| 180 |
练习册系列答案
提分百分百检测卷单元期末测试卷系列答案
小学期末标准试卷系列答案
相关题目
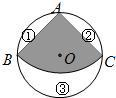如图，从一个直径是2的圆形铁皮中剪下一个圆心角为90°的扇形
如图，从一个直径是1m的圆形铁皮中剪出一个圆心角为90°的扇形．
