题目内容
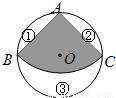
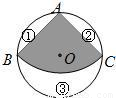
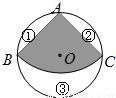
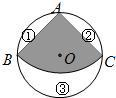 如图,从一个直径是2的圆形铁皮中剪下一个圆心角为90°的扇形
如图,从一个直径是2的圆形铁皮中剪下一个圆心角为90°的扇形(1)求这个扇形的面积(结果保留π)
(2)在剩下的三块余料中,能否从第③块余料中剪出一个圆作为底面与此扇形围成一个圆锥?请说明理由
(3)当⊙O的半径R(R>0)为任意值时,(2)中的结论是否仍然成立?请说明理由.
分析:(1)由勾股定理求扇形的半径,再根据弧长公式求值.
(2)本题需要求出③中最大圆的直径以及圆锥底面圆的直角(圆锥底面圆的周长即弧BC的长).然后进行比较即可.
(3)同(2),需要求出底面半径和剩下的料的最短边之间的大小关系.
(2)本题需要求出③中最大圆的直径以及圆锥底面圆的直角(圆锥底面圆的周长即弧BC的长).然后进行比较即可.
(3)同(2),需要求出底面半径和剩下的料的最短边之间的大小关系.
解答: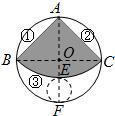 解:(1)连接BC,
解:(1)连接BC,
∵∠A=90°,
∴BC为直径,
∴BC过圆心O,
由勾股定理求得:AB=AC=
,
S=
=
π;
(2)连接AO并延长,与弧BC和⊙O交于E、F,
∵AB=AC,BO=CO,
∴AO⊥BC,
∴EF=AF-AE=2-
,
弧BC的长:l=
=
π;
∵2πr=
π,
∴圆锥的底面直径为:2r=
;
∵2-
<
,
∴不能在余料③中剪出一个圆作为底面与此扇形围成圆锥.
(3)由勾股定理求得:AB=AC=
R;
弧BC的长:l=
=
πR,
∵2πr=
πR,
∴圆锥的底面直径为:2r=
R;
EF=AF-AE=2R-
R=(2-
)R,
∵2-
<
且R>0;
∴(2-
)R<
R.
即无论半径R为何值,EF<2r.
∴不能在余料③中剪出一个圆作为底面与此扇形围成圆锥.
 解:(1)连接BC,
解:(1)连接BC,∵∠A=90°,
∴BC为直径,
∴BC过圆心O,
由勾股定理求得:AB=AC=
| 2 |
S=
| nπR2 |
| 360 |
| 1 |
| 2 |
(2)连接AO并延长,与弧BC和⊙O交于E、F,
∵AB=AC,BO=CO,
∴AO⊥BC,
∴EF=AF-AE=2-
| 2 |
弧BC的长:l=
| nπR |
| 180 |
| ||
| 2 |
∵2πr=
| ||
| 2 |
∴圆锥的底面直径为:2r=
| ||
| 2 |
∵2-
| 2 |
| ||
| 2 |
∴不能在余料③中剪出一个圆作为底面与此扇形围成圆锥.
(3)由勾股定理求得:AB=AC=
| 2 |
弧BC的长:l=
| nπR |
| 180 |
| ||
| 2 |
∵2πr=
| ||
| 2 |
∴圆锥的底面直径为:2r=
| ||
| 2 |
EF=AF-AE=2R-
| 2 |
| 2 |
∵2-
| 2 |
| ||
| 2 |
∴(2-
| 2 |
| ||
| 2 |
即无论半径R为何值,EF<2r.
∴不能在余料③中剪出一个圆作为底面与此扇形围成圆锥.
点评:此题的关键是熟悉圆锥的展开图和底面圆与圆锥的关系.利用所学的勾股定理、弧长公式及扇形面积公式求值.

练习册系列答案
相关题目
 如图,从一个直径是1m的圆形铁皮中剪出一个圆心角为90°的扇形.
如图,从一个直径是1m的圆形铁皮中剪出一个圆心角为90°的扇形.