题目内容
已知如图,AB=AC,∠BAC=90°,AE是过A点的一条直线,且B、C在DE的异侧,BD⊥AE于D,CE⊥AE于E,
(1)△ABD与△CAE全等吗?请说明理由。
(2)判断BD与DE+CE关系,并请说明理由。
(1)△ABD与△CAE全等吗?请说明理由。
(2)判断BD与DE+CE关系,并请说明理由。
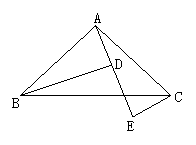
解:(1)△ABD≌ △CAE 理由是:
∵ BD⊥AE CE⊥AE ( 已知)
∴∠ADB=∠AEC= (垂直的定义)
∴∠ABD+∠BAD= ( 直角三角形两锐角互余)
∵∠BAD+∠EAC =∠BAC=( 已知)
∴ ∠ABD=∠EAC( 同角的余角相等)
在△ABD和△CAE中

∴ △ABD≌△CAE (AAS)
(2)BD=DE+CE 理由是:
∵△ABD≌△CAE
∴ AD=CE BD=AE (全等三角形对应边相等)
∴AE= DE+AD= DE+CE
即 BD=DE+CE
∵ BD⊥AE CE⊥AE ( 已知)
∴∠ADB=∠AEC= (垂直的定义)
∴∠ABD+∠BAD= ( 直角三角形两锐角互余)
∵∠BAD+∠EAC =∠BAC=( 已知)
∴ ∠ABD=∠EAC( 同角的余角相等)
在△ABD和△CAE中

∴ △ABD≌△CAE (AAS)
(2)BD=DE+CE 理由是:
∵△ABD≌△CAE
∴ AD=CE BD=AE (全等三角形对应边相等)
∴AE= DE+AD= DE+CE
即 BD=DE+CE

练习册系列答案
相关题目
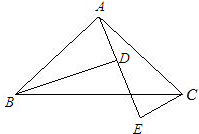 已知如图,AB=AC,∠BAC=90°,AE是过A点的一条直线,且B、C在DE的异侧,BD⊥AE于D,CE⊥AE于E.
已知如图,AB=AC,∠BAC=90°,AE是过A点的一条直线,且B、C在DE的异侧,BD⊥AE于D,CE⊥AE于E.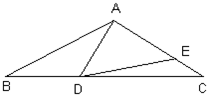
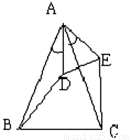
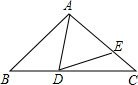 已知如图,AB=AC,AD=AE,若∠BAD=47°30′,求∠CDE的度数.
已知如图,AB=AC,AD=AE,若∠BAD=47°30′,求∠CDE的度数.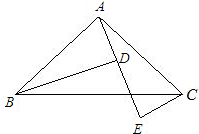 已知如图,AB=AC,∠BAC=90°,AE是过A点的一条直线,且B、C在DE的异侧,BD⊥AE于D,CE⊥AE于E.
已知如图,AB=AC,∠BAC=90°,AE是过A点的一条直线,且B、C在DE的异侧,BD⊥AE于D,CE⊥AE于E.