题目内容
23、已知如图，AB=AC，AD=AE，若∠BAD=47°30′，求∠CDE的度数．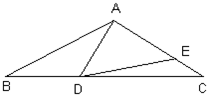
分析：可以设∠EDC=x，∠B=∠C=y，根据∠ADE=∠AED=x+y，∠ADC=∠B+∠BAD即可列出方程，从而求解．
解答：解：设∠EDC=x，∠B=∠C=y，
则∠AED=∠EDC+∠C=x+y，
又因为AD=AE，所以∠ADE=∠AED=x+y，
则∠ADC=∠ADE+∠EDC=2x+y，
又因为∠ADC=∠B+∠BAD，
所以 2x+y=y+47°30′，
解得x=23°45′，
所以∠EDC的度数是23°45′．
则∠AED=∠EDC+∠C=x+y，
又因为AD=AE，所以∠ADE=∠AED=x+y，
则∠ADC=∠ADE+∠EDC=2x+y，
又因为∠ADC=∠B+∠BAD，
所以 2x+y=y+47°30′，
解得x=23°45′，
所以∠EDC的度数是23°45′．
点评：本题主要考查了等腰三角形等边对等角的性质．正确确定相等关系列出方程是解题的关键．
练习册系列答案
相关题目
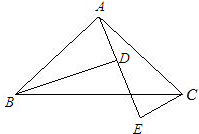已知如图，AB=AC，∠BAC=90°，AE是过A点的一条直线，且B、C在DE的异侧，BD⊥AE于D，CE⊥AE于E．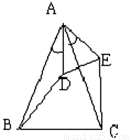
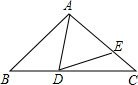已知如图，AB=AC，AD=AE，若∠BAD=47°30′，求∠CDE的度数．
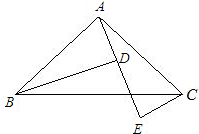已知如图，AB=AC，∠BAC=90°，AE是过A点的一条直线，且B、C在DE的异侧，BD⊥AE于D，CE⊥AE于E．