题目内容
16．在下列图形中，既是轴对称图形又是中心对称图形的是（ ）| A． |  | B． |  | C． |  | D． |  |
分析 根据轴对称图形与中心对称图形的概念求解．
解答 解：A、是轴对称图形，不是中心对称图形．故错误；
B、不是轴对称图形，也不是中心对称图形．故错误；
C、是轴对称图形，也是中心对称图形．故正确；
D、不是轴对称图形，是中心对称图形．故错误．
故选C．
点评 本题考查了中心对称图形与轴对称图形的概念：轴对称图形的关键是寻找对称轴，图形两部分沿对称轴折叠后可重合；中心对称图形是要寻找对称中心，旋转180度后与原图重合．
练习册系列答案
阅读快车系列答案
相关题目
6．下列说法正确的是（ ）
| A． | 单项式y的次数是1，系数是0 | B． | 多项式$\frac{3（1-{x}^{2}）}{8}$中x2的系数是-$\frac{3}{8}$ | ||
| C． | 多项式t-5的项是t和5 | D． | $\frac{xy-1}{2}$是二次单项式 |
4．如图①是4×4正方形方格，已有两个正方形方格被涂黑，请你再将其中两个方格涂黑，并且使得涂黑后的整个图案是轴对称图形，约定经过旋转后全等的图案都视为同一种，图②中的两幅图就视为同一种，则得到的不同图案共有（ ）
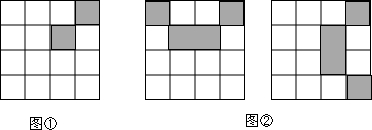
| A． | 6种 | B． | 7种 | C． | 8种 | D． | 9种 |
1．
如图，△ABC中，AB=AC=2，∠BAC=45°，△AEF是由△ABC绕点A按逆时针方向旋转得到的，连接BE、CF相交于点D．
（1）求证：BE=CF；
（2）当四边形ABDF为菱形时，求CD的长．
如图，△ABC中，AB=AC=2，∠BAC=45°，△AEF是由△ABC绕点A按逆时针方向旋转得到的，连接BE、CF相交于点D．（1）求证：BE=CF；
（2）当四边形ABDF为菱形时，求CD的长．
5．根据下列表格的对应值：判断方程ax2+bx+c=0一个解的取值范围是（ ）
| x | 0.59 | 0.60 | 0.61 | 0.62 | 0.63 |
| ax2+bx+c | -0.0619 | -0.04 | -0.0179 | 0.0044 | 0.0269 |
| A． | 0.59＜x＜0.61 | B． | 0.60＜x＜0.61 | C． | 0.61＜x＜0.62 | D． | 0.62＜x＜0.63 |