题目内容
14.求下列函数自变量取值范围(1)y=$\frac{1}{x-2}$;(2)y=$\sqrt{2x-1}$;y=$\frac{\sqrt{3-x}}{x+2}$.
分析 (1)根据分母不等于0列式计算即可得解;
(2)根据被开方数大于等于0列式计算即可得解;
(3)根据被开方数大于等于0,分母不等于0列式计算即可得解.
解答 解:(1)由题意得,x-2≠0,
解得x≠2;
(2)由题意得,2x-1≥0,
解得x≥$\frac{1}{2}$;
(3)由题意得,3-x≥0且x+2≠0,
解得x≤3且x≠-2.
点评 本题考查了函数自变量的范围,一般从三个方面考虑:(1)当函数表达式是整式时,自变量可取全体实数;(2)当函数表达式是分式时,考虑分式的分母不能为0;
(3)当函数表达式是二次根式时,被开方数非负.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
4.某检修小组从O地出发,在东西向的马路上检修线路,如果规定向东行驶为正,向西为负,一天中七次行驶纪录如表.(单位:km)
(1)画数轴表示出每次结束时的点的位置(用表格中的字母表示),并求出收工时距A地多远?
(2)在第五 次纪录时距A地最远.
(3)若每千米耗油0.3升,问共耗油多少升?
| 第一次A | 第二次B | 第三次C | 第四次D | 第五次E | 第六次F | 第七次 G |
| -4 | +7 | -9 | +8 | +6 | -5 | -2 |
(2)在第五 次纪录时距A地最远.
(3)若每千米耗油0.3升,问共耗油多少升?
9.函数y=kx2+mx+n是二次函数,则( )
| A. | k=0,m≠0,n≠0 | B. | k≠0,m≠0,n=0 | C. | k≠0 | D. | 以上都不正确 |
4. 如图,点C是以AB为直径的半圆型铁片上的靠近B点的一个定点,将该铁片按图中的位置斜靠在坐标轴上,现点A沿着y轴向终点O滑动,同时点B相应地沿着x轴向x轴正方向滑动,在滑动过程中,点C与原点O距离的变化情况是( )
如图,点C是以AB为直径的半圆型铁片上的靠近B点的一个定点,将该铁片按图中的位置斜靠在坐标轴上,现点A沿着y轴向终点O滑动,同时点B相应地沿着x轴向x轴正方向滑动,在滑动过程中,点C与原点O距离的变化情况是( )
 如图,点C是以AB为直径的半圆型铁片上的靠近B点的一个定点,将该铁片按图中的位置斜靠在坐标轴上,现点A沿着y轴向终点O滑动,同时点B相应地沿着x轴向x轴正方向滑动,在滑动过程中,点C与原点O距离的变化情况是( )
如图,点C是以AB为直径的半圆型铁片上的靠近B点的一个定点,将该铁片按图中的位置斜靠在坐标轴上,现点A沿着y轴向终点O滑动,同时点B相应地沿着x轴向x轴正方向滑动,在滑动过程中,点C与原点O距离的变化情况是( )| A. | 一直增大 | B. | 保持不变 | C. | 先增大后减小 | D. | 先减小后增大 |
11.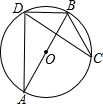 如图,D、C是⊙O上的两点,AB经过圆心O,若∠C=30°,AD=3,则⊙O的直径为( )
如图,D、C是⊙O上的两点,AB经过圆心O,若∠C=30°,AD=3,则⊙O的直径为( )
 如图,D、C是⊙O上的两点,AB经过圆心O,若∠C=30°,AD=3,则⊙O的直径为( )
如图,D、C是⊙O上的两点,AB经过圆心O,若∠C=30°,AD=3,则⊙O的直径为( )| A. | $\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | 3 | D. | 6 |
8.下列四个式子中,是方程的是( )
| A. | 3+2=5 | B. | a2+2ab+b2 | C. | 2x-3 | D. | x=1 |
9.下列实数是负数的是( )
| A. | $\sqrt{2}$ | B. | 3 | C. | 0 | D. | -1 |
 如图,已知圆环的外圆半径为46mm,内圆半径为27mm,求圆环的面积.(π取3.14,结果保留2个有效数字)
如图,已知圆环的外圆半径为46mm,内圆半径为27mm,求圆环的面积.(π取3.14,结果保留2个有效数字)