题目内容
已知:如图,一座商场大楼的顶部竖直立有一个矩形广告牌,小红同学在地面上选择了在一条直线上的三点A(A为楼底)、D、E,她在D处测得广告牌顶端C的仰角为60°,在E两处测得商场大楼楼顶B 的仰角为45°,DE=5米。已知,广告牌的高度BC=2.35米,求这座商场大楼的高度AB( 取1.73,
取1.73, 取1.41,小红的身高不计,结果保留整数)。
取1.41,小红的身高不计,结果保留整数)。
 取1.73,
取1.73, 取1.41,小红的身高不计,结果保留整数)。
取1.41,小红的身高不计,结果保留整数)。
解:设AB为x米。
依题意,在Rt△ABE中, ∠BEA=45°,
∴ AE=AB=x。
∴ AD =AE-DE=x-5,AC = BC+ AB =2.35+x。
在Rt△ADC中, ∠CDA=60°,
∴
∴ x+2.35= (x-5)
(x-5)
∴
解得
∴ x≈15。

答:商场大楼的高度AB约为15米。
依题意,在Rt△ABE中, ∠BEA=45°,
∴ AE=AB=x。
∴ AD =AE-DE=x-5,AC = BC+ AB =2.35+x。
在Rt△ADC中, ∠CDA=60°,
∴

∴ x+2.35=
 (x-5)
(x-5)∴

解得

∴ x≈15。

答:商场大楼的高度AB约为15米。

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目
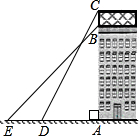 已知:如图,一座商场大楼的顶部竖直立有一个矩形广告牌,小红同学在地面上选择了在一条直线上的三点A(A为楼底)、D、E,她在D处测得广告牌顶端C的仰角为60°,在E两处测得商场大楼楼顶B 的仰角为45°,DE=5米.已知,广告牌的高度BC=2.35米,求这座商场大楼的高度AB(
已知:如图,一座商场大楼的顶部竖直立有一个矩形广告牌,小红同学在地面上选择了在一条直线上的三点A(A为楼底)、D、E,她在D处测得广告牌顶端C的仰角为60°,在E两处测得商场大楼楼顶B 的仰角为45°,DE=5米.已知,广告牌的高度BC=2.35米,求这座商场大楼的高度AB( 已知:如图,一座商场大楼的顶部竖直立有一个矩形广告牌,小红同学在地面上选择了在一条直线上的三点A(A为楼底)、D、E,她在D处测得广告牌顶端C的仰角为60°,在E两处测得商场大楼楼顶B 的仰角为45°,DE=5米.已知,广告牌的高度BC=2.35米,求这座商场大楼的高度AB(
已知:如图,一座商场大楼的顶部竖直立有一个矩形广告牌,小红同学在地面上选择了在一条直线上的三点A(A为楼底)、D、E,她在D处测得广告牌顶端C的仰角为60°,在E两处测得商场大楼楼顶B 的仰角为45°,DE=5米.已知,广告牌的高度BC=2.35米,求这座商场大楼的高度AB( 取1.73,
取1.73, 取1.41,小红的身高不计,结果保留整数).
取1.41,小红的身高不计,结果保留整数).
 取1.73,
取1.73, 取1.41,小红的身高不计,结果保留整数).
取1.41,小红的身高不计,结果保留整数).