题目内容
14.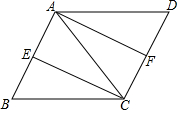 如图所示,已知四边形ABCD是平行四边形,CE,AF分别平分∠BCA,∠CAD.
如图所示,已知四边形ABCD是平行四边形,CE,AF分别平分∠BCA,∠CAD.(1)求证:△BCE≌△DAF;
(2)若AC=BC,求证:四边形AECF是矩形.
分析 (1)只要证明BC=AD,∠B=∠D,∠BCE=∠DAF即可解决问题;
(2)首先证明四边形AECF是平行四边形,再证明CE⊥AB即可;
解答  证明:(1)∵四边形ABCD是平行四边形,
证明:(1)∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,∠B=∠D,
∴∠DAC=∠ACB,
∵CE,AF分别平分∠BCA,∠CAD,
∴∠DAF=$\frac{1}{2}$∠DAC,∠BCE=$\frac{1}{2}$∠BCA,
∴∠DAF=∠BCE,
在△BCE和△DAF中,
$\left\{\begin{array}{l}{∠B=∠D}\\{BC=DA}\\{∠BCE=∠DAF}\end{array}\right.$,
∴△BCE≌△DAF.
(2)∵△BCE≌△DAF,
∴EC=AF,BE=DF,
∵AB=CD,
∴AE=CF,
∴四边形AECF是平行四边形,
∵CA=CB,CE平分∠ACB,
∴CE⊥AB,
∴∠AEC=90°,
∴四边形AECF是矩形.
点评 本题考查平行四边形的判定和性质、矩形的判定和性质、全等三角形的判定和性质等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.

练习册系列答案
相关题目
6.某校随机抽查了10名参加2017年云南省初中学业水平考试学生的体育成绩,得到的结果如表:
下列说法正确的是( )
| 成绩(分) | 46 | 47 | 48 | 49 | 50 |
| 人数(人) | 1 | 2 | 1 | 2 | 4 |
| A. | 这10名同学的体育成绩的平均数为48 | |
| B. | 这10名同学的体育成绩的中位数为48 | |
| C. | 这10名同学的体育成绩的方差为50 | |
| D. | 这10名同学的体育成绩的众数为50 |
 如图,△ABC的边BC的垂直平分线MN交AC于点D,若△ADB的周长是10cm,AB=4cm,求AC的长.
如图,△ABC的边BC的垂直平分线MN交AC于点D,若△ADB的周长是10cm,AB=4cm,求AC的长.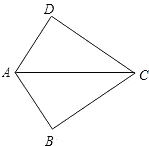 如图所示,∠D=∠B=90°,请你添加一个适当的条件AB=AD,使△ABC≌△ADC.(只需添加一个即可)
如图所示,∠D=∠B=90°,请你添加一个适当的条件AB=AD,使△ABC≌△ADC.(只需添加一个即可) 如图,在△ABC中,∠ACB=90°,AC=BC,BD⊥CE于D,AE⊥CE于E,DE=4cm,BD=6cm,则AE的长是2cm.
如图,在△ABC中,∠ACB=90°,AC=BC,BD⊥CE于D,AE⊥CE于E,DE=4cm,BD=6cm,则AE的长是2cm.