题目内容
18. 如图,在△ABC中,∠BAC=90°,AD⊥BC于D,AC+CD=BD,若CD=1,则BD=3.
如图,在△ABC中,∠BAC=90°,AD⊥BC于D,AC+CD=BD,若CD=1,则BD=3.
分析 在DB上取一点E使得DE=DC,因为AD⊥EC,所以AE=AC,因为AC+CD=BD得AE=BE,再证明AE=EC问题就解决了.
解答 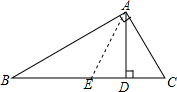 解:在DB上取一点E使得DE=DC,
解:在DB上取一点E使得DE=DC,
∵AD⊥BC,
∴AE=AC,
∵AC+CD=BD,BD=BE+ED,
∴AC=BE=AE,
∴∠B=∠BAE,
∵∠BAC=90°,
∴∠B+∠C=90°,∠BAE+∠EAC=90°,
∴∠EAC=∠C,
∴EA=EC,
∵CD=1,
∴AC=AE=EC=BE=2,
∴BD=BE+ED=2+1=3,
故答案为3.
点评 本题考查等腰三角形的判定和性质、直角三角形的性质、同角的余角相等等知识,添加辅助线构造等腰三角形是解题的关键.

练习册系列答案
 学习实践园地系列答案
学习实践园地系列答案
相关题目
13.如果x+$\frac{1}{x}$=2,则$\frac{{x}^{2}}{2{x}^{4}{+x}^{2}+2}$的值为( )
| A. | $\frac{1}{5}$ | B. | 5 | C. | $\frac{1}{2}$ | D. | $\frac{1}{3}$ |
8.已知a是有理数,则下列结论正确的是( )
| A. | a≥0 | B. | |a|>0 | C. | -a<0 | D. | |a|≥0 |
 如图,一次函数y=-$\frac{1}{2}$x+2分别交y轴、x轴于A、B两点,抛物线y=-x2+bx+c过A、B两点.点N为抛物线上一个动点,过点N作x轴的垂线交直线AB于M,作NE∥x轴交AB于点E,设点N的横坐标为x,△NEM的周长为L.
如图,一次函数y=-$\frac{1}{2}$x+2分别交y轴、x轴于A、B两点,抛物线y=-x2+bx+c过A、B两点.点N为抛物线上一个动点,过点N作x轴的垂线交直线AB于M,作NE∥x轴交AB于点E,设点N的横坐标为x,△NEM的周长为L. 如图,在正方形网格上的一个三角形ABC.(其中点A,B,C均在网格上)
如图,在正方形网格上的一个三角形ABC.(其中点A,B,C均在网格上) 某中心校为迎接县教研室举行的师生写字比赛,对教师组进行了预赛,将各位教师成绩划分为A、B、C、D四个等级,绘制了两种不完整的统计图.
某中心校为迎接县教研室举行的师生写字比赛,对教师组进行了预赛,将各位教师成绩划分为A、B、C、D四个等级,绘制了两种不完整的统计图.