题目内容
12. 如图,对称轴为直线x=2的抛物线y=x2+bx+c与x轴交于点A和点B,与y轴交于点C,且点A的坐标为(-1,0)
如图,对称轴为直线x=2的抛物线y=x2+bx+c与x轴交于点A和点B,与y轴交于点C,且点A的坐标为(-1,0)(1)求抛物线的解析式;
(2)直接写出B、C两点的坐标;
(3)求过O,B,C三点的圆的面积.(结果用含π的代数式表示)
注:二次函数y=ax2+bx+c(a≠0)的顶点坐标为(-$\frac{b}{2a}$,$\frac{4ac-b^2}{4a}$)
分析 (1)利用对称轴方程可求得b,把点A的坐标代入可求得c,可求得抛物线的解析式;
(2)根据A、B关于对称轴对称可求得点B的坐标,利用抛物线的解析式可求得B点坐标;
(3)根据B、C坐标可求得BC长度,由条件可知BC为过O、B、C三点的圆的直径,可求得圆的面积.
解答 解:
(1)由A(-1,0),对称轴为x=2,可得$\left\{\begin{array}{l}{-\frac{b}{2}=2}\\{1-b+c=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{b=-4}\\{c=-5}\end{array}\right.$,
∴抛物线解析式为y=x2-4x-5;
(2)由A点坐标为(-1,0),且对称轴方程为x=2,可知AB=6,
∴OB=5,
∴B点坐标为(5,0),
∵y=x2-4x-5,
∴C点坐标为(0,-5);
(3)如图,连接BC,则△OBC是直角三角形,
∴过O、B、C三点的圆的直径是线段BC的长度,
在Rt△OBC中,OB=OC=5,
∴BC=5$\sqrt{2}$,
∴圆的半径为$\frac{5\sqrt{2}}{2}$,
∴圆的面积为π($\frac{5\sqrt{2}}{2}$)2=$\frac{25}{2}$π.
点评 本题为二次函数的综合应用,涉及知识点有二次函数的性质、待定系数法、勾股定理、圆周角定理等.在(3)中确定出圆的半径是解题的关键.本题属于基础性的题目,难度不大.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.下列运算正确的是( )
| A. | m6÷m2=m3 | B. | 3m2-2m2=m2 | C. | (3m2)3=9m6 | D. | $\frac{1}{2}$m•2m2=m2 |
20.若关于x的分式方程$\frac{x}{x-2}$=2-$\frac{m}{2-x}$的解为正数,则满足条件的正整数m的值为( )
| A. | 1,2,3 | B. | 1,2 | C. | 1,3 | D. | 2,3 |
17. 如图,在平行线a,b之间放置一块直角三角板,三角板的顶点A,B分别在直线a,b上,则∠1+∠2的值为( )
如图,在平行线a,b之间放置一块直角三角板,三角板的顶点A,B分别在直线a,b上,则∠1+∠2的值为( )
 如图,在平行线a,b之间放置一块直角三角板,三角板的顶点A,B分别在直线a,b上,则∠1+∠2的值为( )
如图,在平行线a,b之间放置一块直角三角板,三角板的顶点A,B分别在直线a,b上,则∠1+∠2的值为( )| A. | 90° | B. | 85° | C. | 80° | D. | 60° |
1.下列图形中,既是轴对称图形又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
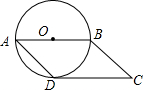 如图,若以平行四边形一边AB为直径的圆恰好与对边CD相切于点D,则∠C=45度.
如图,若以平行四边形一边AB为直径的圆恰好与对边CD相切于点D,则∠C=45度.