题目内容
（2013•莲湖区一模）如图工程上常用钢珠来测量零件上小圆孔的宽口，假设钢珠的直径是10mm，测得钢珠顶端离零件表面的距离为8mm，如图所示．则这个小圆孔的宽口AB的长度是（ ）分析：连接AB，OA，过点O作OD⊥AB于点D，先根据钢珠的直径是10mm，钢珠顶端离零件表面的距离为8mm求出OA及OD的长，再根据勾股定理即可求出AD的长，由垂径定理即可得出结论．
解答：
解：连接AB，OA，过点O作OD⊥AB于点D，
∵钢珠的直径是10mm，钢珠顶端离零件表面的距离为8mm，
∴OA=5mm，OD=8-5=3mm，
∵OD⊥AB，
∴在Rt△OAD中，AD=
=
=4mm，
∴AB=2AD=8mm．
故选C．
解：连接AB，OA，过点O作OD⊥AB于点D，∵钢珠的直径是10mm，钢珠顶端离零件表面的距离为8mm，
∴OA=5mm，OD=8-5=3mm，
∵OD⊥AB，
∴在Rt△OAD中，AD=
| OA2-OD2 |
| 52-32 |
∴AB=2AD=8mm．
故选C．
点评：本题考查的是垂径定理在实际生活中的应用，根据题意作出辅助线，构造出直角三角形是解答此题的关键．
练习册系列答案
相关题目
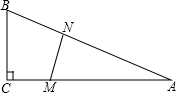（2013•莲湖区一模）如图，在△ABC中，∠C=90°，BC=5米，AC=12米．M点在线段CA上，从C向A运动，速度为1米/秒；同时N点在线段AB上，从A向B运动，速度为2米/秒．△AMN的最大面积是
（2013•莲湖区一模）如图，在正方形ABCD中，E是AB上一点，G是AD上一点，AE=AG，那么CE=CG吗？说明理由．