题目内容
（2013•莲湖区一模）如图，在正方形ABCD中，E是AB上一点，G是AD上一点，AE=AG，那么CE=CG吗？说明理由．分析：由四边形ABCD是正方形，得到AB=AD，结合AE=AG，得到BE=DG，进而证明Rt△CBE≌Rt△CDG，于是得到CE=CG．
解答：解：∵四边形ABCD是正方形，
∴AB=AD，
∵AE=AG，
∴BE=DG，
∵在Rt△CBE和Rt△CDG中，
，
∴Rt△CBE≌Rt△CDG（HL），
∴CE=CG．
∴AB=AD，
∵AE=AG，
∴BE=DG，
∵在Rt△CBE和Rt△CDG中，
|
∴Rt△CBE≌Rt△CDG（HL），
∴CE=CG．
点评：本题主要考查正方形的性质，解答本题的关键是熟练掌握全等三角形的判定与性质定理，此题基础题，比较简单．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
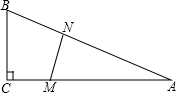（2013•莲湖区一模）如图，在△ABC中，∠C=90°，BC=5米，AC=12米．M点在线段CA上，从C向A运动，速度为1米/秒；同时N点在线段AB上，从A向B运动，速度为2米/秒．△AMN的最大面积是