题目内容
在Rt△ABC中，∠C=90°，sinA=
．
（1）若AB=10，则BC= ，AC= ，cosA= ；
（2）若BC=3x，则AB= ，AC= ，tanA= ，tanB= ，sinB= ；
（3）用计算器可以求得∠A≈ ，∠B≈ （精确到1″）．
| 3 |
| 5 |
（1）若AB=10，则BC=
（2）若BC=3x，则AB=
（3）用计算器可以求得∠A≈
考点：解直角三角形,计算器—三角函数
专题：计算题
分析：（1）利用∠A正弦计算出BC=6，再利用勾股定理计算出AC=6，然后根据余弦的定义求∠B的余弦；
（2）利用∠A正弦得到AB=5x，再利用勾股定理计算出AC=4x，然后根据锐角三角函数的定义求解；
（3）用计算器可得到∠A≈36°52′12″，然后利用互余计算∠B．
（2）利用∠A正弦得到AB=5x，再利用勾股定理计算出AC=4x，然后根据锐角三角函数的定义求解；
（3）用计算器可得到∠A≈36°52′12″，然后利用互余计算∠B．
解答：解：（1）∵sinA=
，
∴BC=10×
=6，
∴AC=
=
=8，
∴cosA=
=
=
；
（2）∵sinA=
，
∴AB=
=5x，
∴AC=
=4x，
∴tanA=
=
=
，tanB=
=
=
，sinB=
=
=
；
（3）∵sinA=
，
∴∠A≈36°52′12″，
∴∠B=90°-∠A=53°7′48″．
故答案6，8，
；5x，4x，
，
，
；36°52′12″，53°7′48″．
| BC |
| AB |
∴BC=10×
| 3 |
| 5 |
∴AC=
| AB2-BC2 |
| 102-62 |
∴cosA=
| AC |
| AB |
| 8 |
| 10 |
| 4 |
| 5 |
（2）∵sinA=
| BC |
| AB |
∴AB=
| 3x | ||
|
∴AC=
| AB2-BC2 |
∴tanA=
| BC |
| AC |
| 3x |
| 4x |
| 3 |
| 4 |
| AC |
| BC |
| 4x |
| 3x |
| 4 |
| 3 |
| AC |
| AB |
| 4x |
| 5x |
| 4 |
| 5 |
（3）∵sinA=
| 3 |
| 5 |
∴∠A≈36°52′12″，
∴∠B=90°-∠A=53°7′48″．
故答案6，8，
| 4 |
| 5 |
| 3 |
| 4 |
| 4 |
| 3 |
| 4 |
| 5 |
点评：本题考查了解直角三角形：在直角三角形中，由已知元素求未知元素的过程就是解直角三角形．也考查了等腰三角形的性质．
练习册系列答案
相关题目
如图，在平面直角坐标系中，已知O（0，0），A（4，0），B（4，3）三点．动点P从点O出发，以每秒3个单位的速度，沿△OAB的边OA，AB，BO做匀速运动．动直线l从AB位置出发，以每秒1个单位的速度向x轴负方向作匀速平移运动．若它们同时出发，运动的时间为t（s），当点P运动到点O时，它们都停止运动．当点P在线段OA上运动时，求直线l与以点P为圆心、1为半径的圆相交时t的取值范围．
观察图中的三角形，把它们的标号填入相应横线上．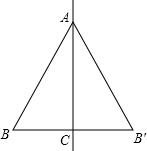
在Rt△ABC中，斜边AB=2BC，以直线AC为对称轴，点B的对称点是B′，如图，则与线段BC相等的线段是