题目内容
18．顺次连接矩形各边中点所得的新四边形的形状是菱形．分析 根据三角形的中位线定理和菱形的判定，顺次连接矩形各边中点所得的四边形是菱形．
解答 
解：如图：E，F，G，H为矩形的中点，则AH=HD=BF=CF，AE=BE=CG=DG，
在Rt△AEH与Rt△DGH中，
$\left\{\begin{array}{l}{AH=DH}\\{∠A=∠D}\\{AE=DG}\end{array}\right.$，
∴△AEH≌△DGH（SAS），
∴EH=HG，
同理，△AEH≌△DGH≌△BEF≌△CGF≌△DGH，
∴EH=HE=GF=EF，∠EHG=∠EFG，
∴四边形EFGH为菱形．
故答案为：菱形．
点评 此题主要考查了菱形的判定，综合利用了三角形的中位线定理和矩形的性质是解题关键．
练习册系列答案
各地期末复习特训卷系列答案
小博士期末闯关100分系列答案
相关题目
8．（1）$\sqrt{2}$+3$\sqrt{2}$-5$\sqrt{2}$
（2）|$\sqrt{3}$-$\sqrt{2}$|+|$\sqrt{3}$-2|+$\sqrt{（-2）^{2}}$．
（2）|$\sqrt{3}$-$\sqrt{2}$|+|$\sqrt{3}$-2|+$\sqrt{（-2）^{2}}$．
6．计算20140的结果是（ ）
| A． | 1 | B． | 0 | C． | 2014 | D． | -1 |
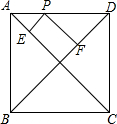如图，在正方形ABCD中，P是AD上任一点，PE⊥AC，PF⊥BD，点E、F分别是垂足，AC=10，则PE+PF的值是（ ）