题目内容
13.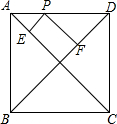 如图,在正方形ABCD中,P是AD上任一点,PE⊥AC,PF⊥BD,点E、F分别是垂足,AC=10,则PE+PF的值是( )
如图,在正方形ABCD中,P是AD上任一点,PE⊥AC,PF⊥BD,点E、F分别是垂足,AC=10,则PE+PF的值是( )| A. | 10 | B. | 5 | C. | 20 | D. | 6 |
分析 由正方形的性质得出∠PAE=45°,OA=$\frac{1}{2}$AC=5,AC⊥BD,证出四边形OEPF是矩形,△PAE是等腰直角三角形,得出PF=OE,PE=AE,得出PE+PF=OA即可.
解答 解:如图所示: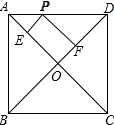 ∵四边形ABCD是正方形,
∵四边形ABCD是正方形,
∴∠PAE=45°,OA=$\frac{1}{2}$AC=5,AC⊥BD,
∴∠AOD=90°,
∵PE⊥AC,PF⊥BD,
∴∠PEA=∠PEO=∠PFO=90°,
∴四边形OEPF是矩形,△PAE是等腰直角三角形,
∴PF=OE,PE=AE,
∴PE+PF=AE+OE=OA=5;
故选:B.
点评 本题考查了正方形的性质、矩形的判定与性质、等腰直角三角形的判定与性质;熟练掌握正方形的性质,并能进行推理计算是解决问题的关键.

练习册系列答案
相关题目
4.直角三角形的两锐角平分线相交成的角的度数是( )
| A. | 45° | B. | 135° | C. | 45°或135° | D. | 以上答案均不对 |
8.直线y=2x-3与直线y=kx+1平行,则k等于( )
| A. | -2 | B. | 2 | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
5.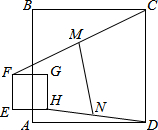 如图,边长为2的正方形EFGH在边长为6的正方形ABCD所在平面上移动,始终保持EF∥AB.线段CF的中点为M,DH的中点为N,则线段MN的长为( )
如图,边长为2的正方形EFGH在边长为6的正方形ABCD所在平面上移动,始终保持EF∥AB.线段CF的中点为M,DH的中点为N,则线段MN的长为( )
 如图,边长为2的正方形EFGH在边长为6的正方形ABCD所在平面上移动,始终保持EF∥AB.线段CF的中点为M,DH的中点为N,则线段MN的长为( )
如图,边长为2的正方形EFGH在边长为6的正方形ABCD所在平面上移动,始终保持EF∥AB.线段CF的中点为M,DH的中点为N,则线段MN的长为( )| A. | $\sqrt{10}$ | B. | $\frac{\sqrt{17}}{2}$ | C. | $\sqrt{17}$ | D. | $\frac{4}{3}$$\sqrt{10}$ |
2.已知数据是1,5,6,5,5,6,6,6,则下面结论正确的是( )
| A. | 平均数是5 | B. | 中位数是5 | C. | 众数是5 | D. | 方差是5 |
 已知在Rt△ABC中,∠B=90°,线段AE、CD分别平分∠BAC、∠ACB,则∠APD的度数为45°.
已知在Rt△ABC中,∠B=90°,线段AE、CD分别平分∠BAC、∠ACB,则∠APD的度数为45°.