题目内容
关于x的方程x2-(m+2)x+(2m-1)=0
(1)求证:方程恒有两个不相等的实数根;
(2)若此方程的一个根为1,求m的值;
(3)求出以此方程两根为直角边的直角三角形的周长.
(1)求证:方程恒有两个不相等的实数根;
(2)若此方程的一个根为1,求m的值;
(3)求出以此方程两根为直角边的直角三角形的周长.
考点:根的判别式,一元二次方程的解,根与系数的关系,勾股定理
专题:
分析:(1)根据关于x的方程x2-(m+2)x+(2m-1)=0的根的判别式的符号来证明结论;
(2)根据一元二次方程的解的定义,将x=1代入方程x2-(m+2)x+(2m-1)=0,即可求得m的值;
(3)先由根与系数的关系求得方程的另一根为3,再分类讨论:①当该直角三角形的两直角边是1、3时,由勾股定理得斜边的长度为:
;②当该直角三角形的直角边和斜边分别是1、3时,由勾股定理得该直角三角形的另一直角边为2
;再根据三角形的周长公式进行计算.
(2)根据一元二次方程的解的定义,将x=1代入方程x2-(m+2)x+(2m-1)=0,即可求得m的值;
(3)先由根与系数的关系求得方程的另一根为3,再分类讨论:①当该直角三角形的两直角边是1、3时,由勾股定理得斜边的长度为:
| 10 |
| 2 |
解答:(1)证明:∵△=(m+2)2-4(2m-1)=(m-2)2+4,
∴在实数范围内,m无论取何值,(m-2)2+4>0,即△>0,
∴关于x的方程x2-(m+2)x+(2m-1)=0恒有两个不相等的实数根;
(2)解:根据题意,得
12-1×(m+2)+(2m-1)=0,
解得,m=2;
(3)解:方程的另一根为:m+2-1=2+1=3;
①当该直角三角形的两直角边是1、3时,由勾股定理得斜边的长度为:
;
该直角三角形的周长为1+3+
=4+
;
②当该直角三角形的直角边和斜边分别是1、3时,由勾股定理得该直角三角形的另一直角边为2
;
则该直角三角形的周长为1+3+2
=4+2
.
∴在实数范围内,m无论取何值,(m-2)2+4>0,即△>0,
∴关于x的方程x2-(m+2)x+(2m-1)=0恒有两个不相等的实数根;
(2)解:根据题意,得
12-1×(m+2)+(2m-1)=0,
解得,m=2;
(3)解:方程的另一根为:m+2-1=2+1=3;
①当该直角三角形的两直角边是1、3时,由勾股定理得斜边的长度为:
| 10 |
该直角三角形的周长为1+3+
| 10 |
| 10 |
②当该直角三角形的直角边和斜边分别是1、3时,由勾股定理得该直角三角形的另一直角边为2
| 2 |
则该直角三角形的周长为1+3+2
| 2 |
| 2 |
点评:本题综合考查了勾股定理、根的判别式、根与系数的关系、一元二次方程解的定义.解答(3)时,采用了“分类讨论”的数学思想.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
等腰三角形的两边长分别为5cm和10cm,则此三角形的周长是( )
| A、25cm |
| B、20cm |
| C、15cm |
| D、20cm或25cm |
一元二次方程(m-2)x2-4mx+2m-6=0有两个相等的实数根,则m等于( )
| A、-6或1 | B、1 | C、-6 | D、2 |
下列说法错误的是( )
| A、1的平方根是1 | ||||
| B、-1的立方根是-1 | ||||
C、
| ||||
D、-
|
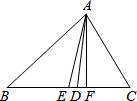 如图,在△ABC中,AE是中线,AD是角平分线,AF是高.则
如图,在△ABC中,AE是中线,AD是角平分线,AF是高.则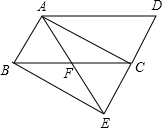 如图,将平行四边形ABCD的边DC延长到点E,使CE=DC,连接AE,交BC于点F.
如图,将平行四边形ABCD的边DC延长到点E,使CE=DC,连接AE,交BC于点F.