题目内容
13. 如图,∠AOB=45°,点C在OB上,OC=8,若以点C为圆心、r为半径的圆与OA相切,则r等于( )
如图,∠AOB=45°,点C在OB上,OC=8,若以点C为圆心、r为半径的圆与OA相切,则r等于( )| A. | 4 | B. | 4$\sqrt{2}$ | C. | 4$\sqrt{3}$ | D. | 8 |
分析 过C点作CD⊥OA,如图,根据切线的性质得CD=r,然后根据等腰直角三角形的性质求CD的长即可.
解答 解:过C点作CD⊥OA,如图,
∵以点C为圆心、r为半径的圆与OA相切,
∴CD=r,
在Rt△OCD中,∵∠COD=45°,
∴CD=$\frac{\sqrt{2}}{2}$OC=$\frac{\sqrt{2}}{2}$×8=4$\sqrt{2}$,
即r=4$\sqrt{2}$.
故选B.
点评 本题考查了切线的性质:圆的切线垂直于经过切点的半径.若出现圆的切线,必连过切点的半径,构造定理图,得出垂直关系.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
3.在式子x2+5,-1,x2-3x+2,π,$\frac{5}{π}$,x2+$\frac{1}{x+1}$中,整式有( )
| A. | 3个 | B. | 4个 | C. | 5个 | D. | 6个 |
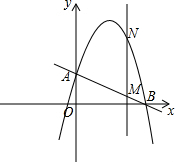 如图,一次函数y=-$\frac{1}{2}$x+2分别交y轴、x轴于A,B两点,抛物线y=-x2+bx+c过A,B两点.
如图,一次函数y=-$\frac{1}{2}$x+2分别交y轴、x轴于A,B两点,抛物线y=-x2+bx+c过A,B两点.