题目内容
如图1所示,在A、B两地之间有汽车站C站,客车由A地驶向C站,货车由B地驶向A地,两车同时出发,匀速行驶,图2是客车、货车离C站的路程y1、y2(千米)与行驶时间x(小时)之间的函数关系图象.

(1)填空:A、B两地相距 千米;
(2)求两小时后,货车离C站的路程y2与行驶时间x之间的函数关系式.
(3)客、货两车何时相遇?
(1) 80+360=440;
80+360=440;
(2)根据图象可知点D(2,0),
∵前两小时货车的速度为80÷2=40(千米/时),
∴货车行驶360千米所需时间为360÷40=9(小时),∴点P(11,360).
利用待定系数法可求得直线DP,即两小时后,货车离C站的路程y2与时间x之间的函数关系式为y2=40x-80;
(3)∵点(6,0)和(0,360)在直线EF上,
∴直线EF的函数关系式为y1 =-60x+360.
=-60x+360.
联立直线DP和EF的函数解析式得方程组
 解得
解得
答:客、货两车4.4小时相遇.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 中,自变量x的取值范围是 .
中,自变量x的取值范围是 .



 x的图象上,则m的值是( )
x的图象上,则m的值是( ) B.-
B.- 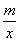 的图象如图所示,以下结论:①常数m<-1;②在每个象限内,y随x的增大而增大;③若A(-1,h),B(2,k)在图象上,则h<k;④若P(x,y)在图象上,则P′(-x,-y)也在图象上.其中正确的是( )
的图象如图所示,以下结论:①常数m<-1;②在每个象限内,y随x的增大而增大;③若A(-1,h),B(2,k)在图象上,则h<k;④若P(x,y)在图象上,则P′(-x,-y)也在图象上.其中正确的是( )
 (x+1)2+3,下
(x+1)2+3,下 列结论:①抛物线的开口向下;②对称轴为直线x=1;③顶点坐标为(-1,3);④x>1
列结论:①抛物线的开口向下;②对称轴为直线x=1;③顶点坐标为(-1,3);④x>1 时,y随x的增大而减小.其中正确结论的个数为( )
时,y随x的增大而减小.其中正确结论的个数为( )