题目内容
如图，△ABC中，∠ACB=90°，AC=AE，∠B=50°，∠BCE=考点：等腰三角形的性质
专题：
分析：由△ABC中，∠ACB=90°，∠B=50°，根据三角形内角和定理，即可求得∠A的度数，又由AC=AE，根据等边对等角的性质，即可求得∠ACE的度数，继而求得答案．
解答：解：∵△ABC中，∠ACB=90°，∠B=50°，
∴∠A=180°-90°-50°=40°，
∵AC=AE，
∴∠ACE=∠AEC=70°，
∴∠BCE=∠ACB-∠ACE=20°．
故答案为：20°．
∴∠A=180°-90°-50°=40°，
∵AC=AE，
∴∠ACE=∠AEC=70°，
∴∠BCE=∠ACB-∠ACE=20°．
故答案为：20°．
点评：此题考查了等腰三角形的性质．此题难度不大，注意掌握数形结合思想的应用．
练习册系列答案
相关题目
如图，将平行四边形ABCD的边BC延长，若∠A=110°，则∠1=（ ）| A、70° | B、80° |
| C、100° | D、110° |
等边△ABC在数轴上的位置如图所示，点A、C对应的数分别为0和-1，若△ABC绕顶点沿顺时针方向在数轴上连续翻转，翻转1次后，点B所对应的数为1，则连续翻转2015次后，点A（ ）
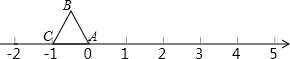
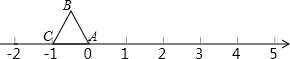
| A、不对应任何数 |
| B、对应的数是2013 |
| C、对应的数是2014 |
| D、对应的数是2015 |
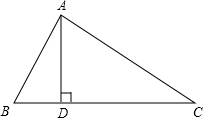在△ABC中，AD是BC边上的高，CD=AB+BD．求证：∠B=2∠C．二次函数y=-x2+2x的图象可能是（ ）
A、 |
B、 |
C、 |
D、 |
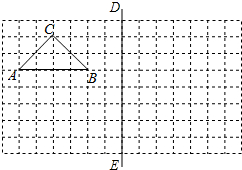如图，在所给网格图（每小格均为边长是1的正方形）中完成下列各题：