题目内容
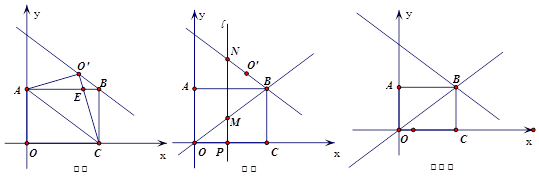
将等腰直角三角形AOB按如图所示放置，然后绕点O逆时针旋转90°至△A′OB′的位置，点B的横坐标为2，则点A′的坐标为 ．
【答案】
(-1,1).
【解析】
试题分析：过点A作AC⊥x轴于点C,过点A′作A′D⊥x轴，因为ΔOAB是等腰直角三角形，所以有OC=BC=AC=1, ∠AOB=∠AOB′=45°，则点A的坐标是（1,1），OA=
,又∠A′OB′=45°，所以∠A′OD=45°，OA′=,在RtΔA′OD中，cos∠A′OD=
,所以OD=1，A′D=1，所以点A′的坐标是（-1,1）.
考点：1、旋转的性质；2、等腰三角形的性质.
练习册系列答案
暑假作业海燕出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目
，试猜想AO，BC有何关系，并证明你的结论，若将△ODB绕顶点D旋转到图(2)、图(3)的位置，上述关系是否仍然成立？若成立，则它表明了几何学中的一个基本事实是________(在横线上填出来)，若不成立，请简要说明理由．
（x＞0）也恰好经过点A．
