题目内容
已知,平面直角坐标系中,矩形OABC的边OC在x轴正半轴上,边OA在y轴正半轴上,B点的坐标为(4,3).将△AOC沿对角线AC所在的直线翻折,得到△AO’C,点O’为点O的对称点,CO’与AB相交于点E(如图①).

(1)试说明:EA=EC;
(2)求直线BO’的解析式;
(3)作直线OB(如图②),直线l平行于y轴,分别交x轴、直线OB、O’B于点P、M、N,设P点的横坐标为m(m>0).y轴上是否存在点F,使得ΔFMN为等腰直角三角形?若存在,请求出此时m的值;若不存在,请说明理由.
【答案】
(1)由折叠的性质可得∠ACO=∠ACE,再根据矩形的性质可得∠EAC=∠ACO,即可得到∠EAC=∠ACE,从而证得结论;(2) ;(3)m=
;(3)m= 、m=
、m= 、m=12
、m=12
【解析】
试题分析:(1)由折叠的性质可得∠ACO=∠ACE,再根据矩形的性质可得∠EAC=∠ACO,即可得到∠EAC=∠ACE,从而证得结论;
(2)先由折叠的性质求得点O’的坐标,即可得到结果;
(3)根据等腰直角三角形的性质结合一次函数的性质即可求得结果.
(1)由题意得∠ACO=∠ACE,
∵矩形OABC
∴AB∥CO
∴∠EAC=∠ACO
∴∠EAC=∠ACE
∴EA=EC;
(2)由题意得点O’的坐标为( ,
, )
)
设函数关系式为
∵图象过点( ,
, ),(4,3)
),(4,3)
 ,解得
,解得
∴函数关系式为 ;
;
(3)当∠FMN=90°时,可得m= ;
;
当∠FNM=90°时,可得m= ;
;
当∠NFM=90°时,可得m=12.
考点:矩形的性质,一次函数的应用
点评:解答本题的关键是熟练掌握折叠的性质:折叠前后的图形的对应边、对应角相等.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
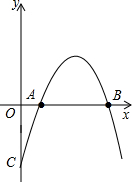 二次函数y=ax2+bx+c(a≠0)的图象经过点A、B,与y轴相交于点C.
二次函数y=ax2+bx+c(a≠0)的图象经过点A、B,与y轴相交于点C. (2013•浙江一模)如图,已知在平面直角坐标系中,点A(4,0)、B(-3,0),点C在y轴正半轴上,且tan∠CAO=1,点Q是线段AB上的动点,过点Q作QE∥AC交BC于点E.
(2013•浙江一模)如图,已知在平面直角坐标系中,点A(4,0)、B(-3,0),点C在y轴正半轴上,且tan∠CAO=1,点Q是线段AB上的动点,过点Q作QE∥AC交BC于点E.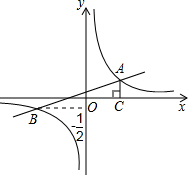 (2012•樊城区模拟)如图,已知在平面直角坐标系xOy中,一次函数y1=kx+b(k≠0)的图象与反比例函数y2=
(2012•樊城区模拟)如图,已知在平面直角坐标系xOy中,一次函数y1=kx+b(k≠0)的图象与反比例函数y2=