题目内容
如图,梯形ABCD是拦水坝的横断面图,(图中i=1: 是指坡面的铅直高度DE与水平宽度CE的比),∠B=60°,AB=6,AD=4,求拦水坝的横断面ABCD的面积.(结果保留三位有效数字.参考数据:
是指坡面的铅直高度DE与水平宽度CE的比),∠B=60°,AB=6,AD=4,求拦水坝的横断面ABCD的面积.(结果保留三位有效数字.参考数据: ≈1.732,
≈1.732, ≈1.414)
≈1.414)
 是指坡面的铅直高度DE与水平宽度CE的比),∠B=60°,AB=6,AD=4,求拦水坝的横断面ABCD的面积.(结果保留三位有效数字.参考数据:
是指坡面的铅直高度DE与水平宽度CE的比),∠B=60°,AB=6,AD=4,求拦水坝的横断面ABCD的面积.(结果保留三位有效数字.参考数据: ≈1.732,
≈1.732, ≈1.414)
≈1.414)
解:过点A作AF⊥BC,垂足为点F.
在Rt△ABF中,∠B=60°,AB=6,
∴AF=ABsin∠B=6sin60°=3 .
.
BF=ABcos∠B=6cos60°=3.
∵AD∥BC,AF⊥BC,DE⊥BC,
∴四边形AFED是矩形,
∴DE=AF=3 ,FE=AD=4.
,FE=AD=4.
在Rt△CDE中,i= ,
,
∴EC= ED=
ED= ×3
×3 =9,
=9,
∴BC=BF+FE+EC=3+4+9=16.
∴S梯形ABCD= (AD+BC)DE=
(AD+BC)DE= (4+16)×3
(4+16)×3 ×52.0.
×52.0.
答:拦水坝的横断面ABCD的面积约为52.0面积单位.
在Rt△ABF中,∠B=60°,AB=6,
∴AF=ABsin∠B=6sin60°=3
 .
.BF=ABcos∠B=6cos60°=3.
∵AD∥BC,AF⊥BC,DE⊥BC,
∴四边形AFED是矩形,
∴DE=AF=3
 ,FE=AD=4.
,FE=AD=4.在Rt△CDE中,i=
 ,
,∴EC=
 ED=
ED= ×3
×3 =9,
=9,∴BC=BF+FE+EC=3+4+9=16.
∴S梯形ABCD=
 (AD+BC)DE=
(AD+BC)DE= (4+16)×3
(4+16)×3 ×52.0.
×52.0.答:拦水坝的横断面ABCD的面积约为52.0面积单位.


练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图等腰梯形ABCD是⊙O的外切四边形,O是圆心,腰长4cm,则∠BOC=
如图等腰梯形ABCD是⊙O的外切四边形,O是圆心,腰长4cm,则∠BOC=
 (2012•凉山州)如图,梯形ABCD是直角梯形.
(2012•凉山州)如图,梯形ABCD是直角梯形.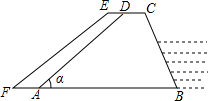 (2012•张家口一模)如图,梯形ABCD是一个拦河坝的截面图,坝高为6米.背水坡AD的坡度i为1:1.2,为了提高河坝的抗洪能力,防汛指挥部决定加固河坝,若坝顶CD加宽0.8米,新的背水坡EF的坡度为1:1.4.河坝总长度为4800米.
(2012•张家口一模)如图,梯形ABCD是一个拦河坝的截面图,坝高为6米.背水坡AD的坡度i为1:1.2,为了提高河坝的抗洪能力,防汛指挥部决定加固河坝,若坝顶CD加宽0.8米,新的背水坡EF的坡度为1:1.4.河坝总长度为4800米. 费用为0.05万元/m2,若设计要求通道宽度x≤8m,则宽度x为多少时,世纪广场修建总费用最少?最少费用为多少?
费用为0.05万元/m2,若设计要求通道宽度x≤8m,则宽度x为多少时,世纪广场修建总费用最少?最少费用为多少?