题目内容
4.已知:抛物线y=x2+(2m-1)x+m2-1经过坐标原点,且当x<0时,y随x的增大而减小.(1)求抛物线的解析式;
(2)结合图象写出,0<x<4时,直接写出y的取值范围-$\frac{9}{4}$≤y<4;
(3)设点A是该抛物线上位于x轴下方的一个动点,过点A作x轴的平行线交抛物线于另一点D,再作AB⊥x轴于点B,DC⊥x轴于点C.当BC=1时,求出矩形ABCD的周长.
分析 (1)把(0,0)代入抛物线解析式求出m的值,再根据增减性确定m的值即可.
(2)画出函数图象,求出函数最小值以及x=0或4是的y的值,由此即可判断.
(3)由BC=1,B、C关于对称轴对称,推出B(,1,0),C((2,0),由AB⊥x轴,DC⊥x轴,推出A(1,-2),D(2,-2),求出AB,即可解决问题.
解答 解:(1)∵y=x2+(2m-1)x+m2-1经过坐标原点,
∴0=0+0+m2-1,即m2-1=0
解得m=±1.
又∵当x<0时,y随x的增大而减小,
∴m=-1,
∴二次函数解析式为y=x2-3x.
(2)如图1中,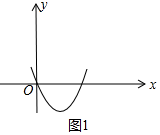
x=0时,y=0,
∵y=(x-$\frac{3}{2}$)2-$\frac{9}{4}$,
∴x=$\frac{3}{2}$时,y最小值为-$\frac{9}{4}$,
x=4时,y=4,
∴0<x<4时,-$\frac{9}{4}$≤y<4.
故答案为-$\frac{9}{4}$≤y<4.
(3)如图2中,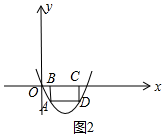
∵BC=1,B、C关于对称轴对称,
∴B(,1,0),C((2,0),
∵AB⊥x轴,DC⊥x轴,
∴A(1,-2),D(2,-2),
∴AB=DC=2,BC=AD=1,
∴四边形ABCD的周长为6,
当BC=1时,矩形的周长为6.
点评 本题考查二次函数的有关性质、矩形的性质等知识,解题的关键是熟练掌握配方法确定函数的顶点坐标,学会根据抛物线的对称性解决问题,属于中考常考题型.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
19.下列式子中成立的是( )
| A. | (-2)2>-32 | B. | -0.3<-$\frac{1}{3}$ | C. | -$\frac{4}{5}$<-$\frac{7}{6}$ | D. | -$\frac{10}{9}$>-$\frac{9}{10}$ |
9.已知点A(-1-$\sqrt{2}$,y1)、B(-1,y2)、C(2,y3)在抛物线y=(x-1)2+c上,则y1、y2、y3的大小关系是( )
| A. | y1>y2>y3 | B. | y1>y3>y2 | C. | y3>y1>y2 | D. | y2>y3>y1 |
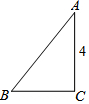 如图,在Rt△ABC中,∠C=90°,AC=4,cosA=$\frac{4}{5}$,则BC=3.
如图,在Rt△ABC中,∠C=90°,AC=4,cosA=$\frac{4}{5}$,则BC=3. 如图是由8个相同的立方体组成的几何体,请分别画出它的主视图、左视图和俯视图.
如图是由8个相同的立方体组成的几何体,请分别画出它的主视图、左视图和俯视图.