题目内容
 如图,从一个直径为2的圆形铁皮中剪下一个圆心角为90°的扇形.
如图,从一个直径为2的圆形铁皮中剪下一个圆心角为90°的扇形.(1)求这个扇形的面积(结果保留π);
(2)在剩下的三块余料中,能否从第③块余料中剪出一个圆作为底面与此扇形围成一个圆锥?说明理由.
分析:(1)连接BC、OA,由于∠BAC=90°,根据圆周角定理知BC为⊙O的直径,根据等腰三角形的性质即可求出AB、AC的长,即扇形的半径长,已知了扇形的圆心角为90°,根据扇形的面积公式即可求出扇形的面积.
(2)过A作⊙O的直径AD,求出以DE为直径的圆的周长,若此圆的周长<弧BC的长,则不能围成圆锥,反之则能.
(2)过A作⊙O的直径AD,求出以DE为直径的圆的周长,若此圆的周长<弧BC的长,则不能围成圆锥,反之则能.
解答: 解:(1)连接BC、AO,并延长AO交⊙O于D,交弧BC于点E,
解:(1)连接BC、AO,并延长AO交⊙O于D,交弧BC于点E,
∵扇形的圆心角为90°,
∴BC为⊙O直径,AB=AC,
∴AO⊥BC,(1分)
在Rt△AOB中,∠AOB=90°,
由勾股定理得:AB=
=
(AB>0),(2分)
∴s=
=
;(3分)
(2)由(1)可知:DE=AD-AE=AD-AB=2-
,
∵弧BC的长l=
=
,
∴2πr=
,
∴2r=
,(4分)
而2-
<
;
∴不能从第③块余料中剪出一个圆作为底面与此扇形围成一个圆锥.(5分)
 解:(1)连接BC、AO,并延长AO交⊙O于D,交弧BC于点E,
解:(1)连接BC、AO,并延长AO交⊙O于D,交弧BC于点E,∵扇形的圆心角为90°,
∴BC为⊙O直径,AB=AC,
∴AO⊥BC,(1分)
在Rt△AOB中,∠AOB=90°,
由勾股定理得:AB=
| AO2+BO2 |
| 2 |
∴s=
| nπR2 |
| 360 |
| π |
| 2 |
(2)由(1)可知:DE=AD-AE=AD-AB=2-
| 2 |
∵弧BC的长l=
| nπR |
| 180 |
| ||
| 2 |
∴2πr=
| ||
| 2 |
∴2r=
| ||
| 2 |
而2-
| 2 |
| ||
| 2 |
∴不能从第③块余料中剪出一个圆作为底面与此扇形围成一个圆锥.(5分)
点评:此题主要考查的了圆周角定理、扇形的面积计算方法、弧长公式等知识.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
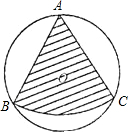 如图,从一个直径为2的圆形铁皮中剪下一个圆心角为60°的扇形ABC,将剪下来的扇形围成一个圆锥,则圆锥的底面圆半径为( )
如图,从一个直径为2的圆形铁皮中剪下一个圆心角为60°的扇形ABC,将剪下来的扇形围成一个圆锥,则圆锥的底面圆半径为( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
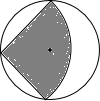 如图,从一个直径为1m的圆形铁片中剪出一个圆心角为90°的扇形,再将剪下的扇形围成一个圆锥,则圆锥的底面半径为
如图,从一个直径为1m的圆形铁片中剪出一个圆心角为90°的扇形,再将剪下的扇形围成一个圆锥,则圆锥的底面半径为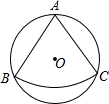 (2012•襄阳)如图,从一个直径为4
(2012•襄阳)如图,从一个直径为4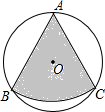 如图,从一个直径为2的圆形铁皮中剪下一个圆心角为60°的扇形ABC,将剪下来的扇形围成一个圆锥,则圆锥的底面圆半径为
如图,从一个直径为2的圆形铁皮中剪下一个圆心角为60°的扇形ABC,将剪下来的扇形围成一个圆锥,则圆锥的底面圆半径为 如图,从一个直径为4的圆形铁片中剪下一个圆心角为90°的扇形ABC.
如图,从一个直径为4的圆形铁片中剪下一个圆心角为90°的扇形ABC.