题目内容
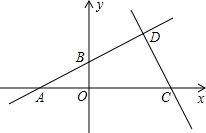 如图,在平面直角坐标系中,点O为坐标原点,A(-4,0),B(0,2),C(6,0),直线AB与直线CD相交于点D,D点横纵坐标相同.
如图,在平面直角坐标系中,点O为坐标原点,A(-4,0),B(0,2),C(6,0),直线AB与直线CD相交于点D,D点横纵坐标相同.(1)求点D的坐标;
(2)点P从O出发,以每秒1个单位的速度沿x轴正半轴匀速运动,过点P作x轴的垂线分别与直线AB、CD交于E、F两点,设点P的运动时间为t秒,线段EF的长为y(y>0),求y与t的函数关系式,并直接写出自变量t的取值范围;
(3)在(2)的条件下,在直线CD上是否存在点Q,使得△BPQ是以点P为直角顶点的等腰直角三角形?若存在,请求出符合条件的Q点坐标;若不存在,请说明理由.
考点:一次函数综合题
专题:
分析:(1)根据条件可求得直线AB的解析式,可设D为(a,a),代入可求得D点坐标;
(2)分0<t<4、4<t≤6和t>6三种情况分别讨论,利用平行线分线段成比例用t表示出PE、PF,可得到y与t的函数关系式;
(3)分0<t<4和t>4,两种情况,过Q作x轴的垂线,证明三角形全等,用t表示出Q点的坐标,代入直线CD,可求得t的值,可得出Q点的坐标.
(2)分0<t<4、4<t≤6和t>6三种情况分别讨论,利用平行线分线段成比例用t表示出PE、PF,可得到y与t的函数关系式;
(3)分0<t<4和t>4,两种情况,过Q作x轴的垂线,证明三角形全等,用t表示出Q点的坐标,代入直线CD,可求得t的值,可得出Q点的坐标.
解答:解:(1)设直线AB的解析式为y=kx+b,
将A(-4,0)、B(0,2)两点代入,
解得,k=
,b=2,
∴直线AB解析式为y=
x+2,
∵D点横纵坐标相同,设D(a,a),
∴a=
a+2,
∴D(4,4);
(2)设直线CD解析式为y=mx+n,
把C、D两点坐标代入,解得m=-2,n=12,
∴直线CD的解析式为y=-2x+12,
∴AB⊥CD,
当 0≤t<4时,如图1,

设直线CD于y轴交于点G,则OG=12,OA=4,OC=6,OB=2,OP=t,
∴PC=6-t,AP=4+t,
∵PF∥OG,
∴
=
,
=
,
∴
=
,
=
,
∴PE=2+
,PF=12-2t,
∴y=PF-PE=-2t+12-(
t+2)=-
t+10,
当4<t≤6时,如图2,

同理可求得PE=2+
,PF=12-2t,
此时y=PE-PF=
t+2-(-2t+12)=
t-10,
当t>6时,如图3,

同理可求得PE=2+
,PF=2t-12,
此时y=PE+PF=
t-10;
综上可知y=
,t的取值范围为:0<t<4或t>4;
(3)存在.
当0<t<4时,过点Q作QM⊥x轴于点M,如图4,

∵∠BPQ=90°,
∴∠BPO+∠QPM=∠OBP+∠BPO=90°,
∴∠OPB=∠QPM,
在△BOP和△PMQ中,
,
∴△BOP≌△PMQ(AAS),
∴BO=PM=2,OP=QM=t,
∴Q(2+t,t),
又Q在直线CD上,
∴t=-2(t+2)+12,
∴t=
,
∴Q(
,
);
当t>4时,过点Q作QN⊥X轴于点N,如图5,

同理可证明△BOP≌△PNQ,
∴BO=PN=2,OP=QN=t,
∴Q(t-2,-t),
又∵Q在直线CD上,
∴-t=-2(t-2)+12,
∴t=16,
∴Q(14,-16),
综上可知,存在符合条件的Q点,其坐标为(
,
)或(14,-16).
将A(-4,0)、B(0,2)两点代入,
解得,k=
| 1 |
| 2 |
∴直线AB解析式为y=
| 1 |
| 2 |
∵D点横纵坐标相同,设D(a,a),
∴a=
| 1 |
| 2 |
∴D(4,4);
(2)设直线CD解析式为y=mx+n,
把C、D两点坐标代入,解得m=-2,n=12,
∴直线CD的解析式为y=-2x+12,
∴AB⊥CD,
当 0≤t<4时,如图1,

设直线CD于y轴交于点G,则OG=12,OA=4,OC=6,OB=2,OP=t,
∴PC=6-t,AP=4+t,
∵PF∥OG,
∴
| PE |
| OB |
| AP |
| AO |
| PF |
| OG |
| PC |
| OC |
∴
| PE |
| 2 |
| 4+t |
| 4 |
| PF |
| 12 |
| 6-t |
| 6 |
∴PE=2+
| t |
| 2 |
∴y=PF-PE=-2t+12-(
| 1 |
| 2 |
| 5 |
| 2 |
当4<t≤6时,如图2,

同理可求得PE=2+
| t |
| 2 |
此时y=PE-PF=
| 1 |
| 2 |
| 5 |
| 2 |
当t>6时,如图3,

同理可求得PE=2+
| t |
| 2 |
此时y=PE+PF=
| 5 |
| 2 |
综上可知y=
|
(3)存在.
当0<t<4时,过点Q作QM⊥x轴于点M,如图4,

∵∠BPQ=90°,
∴∠BPO+∠QPM=∠OBP+∠BPO=90°,
∴∠OPB=∠QPM,
在△BOP和△PMQ中,
|
∴△BOP≌△PMQ(AAS),
∴BO=PM=2,OP=QM=t,
∴Q(2+t,t),
又Q在直线CD上,
∴t=-2(t+2)+12,
∴t=
| 8 |
| 3 |
∴Q(
| 14 |
| 3 |
| 8 |
| 3 |
当t>4时,过点Q作QN⊥X轴于点N,如图5,

同理可证明△BOP≌△PNQ,
∴BO=PN=2,OP=QN=t,
∴Q(t-2,-t),
又∵Q在直线CD上,
∴-t=-2(t-2)+12,
∴t=16,
∴Q(14,-16),
综上可知,存在符合条件的Q点,其坐标为(
| 14 |
| 3 |
| 8 |
| 3 |
点评:本题主要考查待定系数法求函数解析式和平行线分线段成比例、等腰直角三角形的性质、全等三角形的判定和性质等知识点的综合应用.求得点的坐标是利用待定系数法的关键,在(2)中利用t表示出相应线段,化动为静是解题的关键,在(3)中构造三角形全等是解题的关键.本题难度较大,知识点较多,注意分类讨论思想的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,在平面直角坐标系中,直线l经过点A(
如图,在平面直角坐标系中,直线l经过点A( 如图,每个小正方形的边长为1,把阴影部分剪下来,用剪下来的阴影部分拼成一个正方体,那么新正方体的边长是
如图,每个小正方形的边长为1,把阴影部分剪下来,用剪下来的阴影部分拼成一个正方体,那么新正方体的边长是