题目内容
 如图,在平面直角坐标系中,直线l经过点A(
如图,在平面直角坐标系中,直线l经过点A(| 25 |
| 3 |
| 25 |
| 4 |
(1)求直线l的函数解析式;
(2)若给定点M(5,0),存在直线l上的两点P,Q,使得以O,P,Q为顶点的三角形与△OMP全等,请求出所有符合条件的点P的坐标.
考点:一次函数综合题
专题:
分析:(1)根据待定系数法,可得一次函数解析式;
(2)分类讨论:当OP平分∠QOM时,△OMP≌△OQP,可得OM=OQ,根据自变量的值,可得相应的函数值;当OA=PA,OM=PQ时,△OMP≌△PQO,可得PF=OE=5,根据函数值,可得相应自变量的值;当OA=AP,OM=PQ时,△OMP≌△PQO,根据AAS,可得△OEA≌△PFA,可得PF的值,根据函数值,可得相应自变量的值.
(2)分类讨论:当OP平分∠QOM时,△OMP≌△OQP,可得OM=OQ,根据自变量的值,可得相应的函数值;当OA=PA,OM=PQ时,△OMP≌△PQO,可得PF=OE=5,根据函数值,可得相应自变量的值;当OA=AP,OM=PQ时,△OMP≌△PQO,根据AAS,可得△OEA≌△PFA,可得PF的值,根据函数值,可得相应自变量的值.
解答:解:(1)设直线l的函数解析式为y=kx+b,
把点A(
,0),B(0,
)代入解析式y=kx+b,
解得:k=-
,b=
.
故直线l的函数解析式为y=-
x+
;
(2)①如图1,作OQ⊥AB,
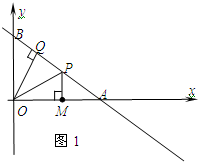
S△AOB=
OA•OB=
AB•OQ.
∴OM=5,
∴OQ=OM.
当OP平分∠QOM时,△OMP≌△OQP,此时PM⊥OA.
把x=5代入y=-
x+
,得y=
.
∴P1(5,
).
②如图2,当OA=PA,OM=PQ时,△OMP≌△PQO,
过O作OE⊥AB于点E,过P作PF⊥OA于点F.
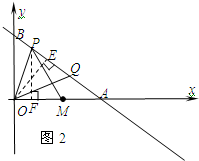
∴△OEA≌△PFA.
∴PF=OE=5.
把 y=5代入y=-
x+
,得x=
.
∴P2(
,5);
③如图3,当OA=AP,OM=PQ时,△OMP≌△PQO.
过O作OE⊥AB于点E,过P作PF⊥OA于点F.
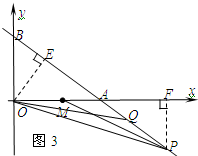
∴△OEA≌△PFA.
PF=OE=-5.
把y=-5代入y=-
x+
,得,x=15.
∴P3(15,-5).
综上所述,所有符合条件的点P的坐标为P1(5,
),P2(
,5),P3(15,-5).
把点A(
| 25 |
| 3 |
| 25 |
| 4 |
解得:k=-
| 3 |
| 4 |
| 25 |
| 4 |
故直线l的函数解析式为y=-
| 3 |
| 4 |
| 25 |
| 4 |
(2)①如图1,作OQ⊥AB,

S△AOB=
| 1 |
| 2 |
| 1 |
| 2 |
∴OM=5,
∴OQ=OM.
当OP平分∠QOM时,△OMP≌△OQP,此时PM⊥OA.
把x=5代入y=-
| 3 |
| 4 |
| 25 |
| 4 |
| 5 |
| 2 |
∴P1(5,
| 5 |
| 2 |
②如图2,当OA=PA,OM=PQ时,△OMP≌△PQO,
过O作OE⊥AB于点E,过P作PF⊥OA于点F.

∴△OEA≌△PFA.
∴PF=OE=5.
把 y=5代入y=-
| 3 |
| 4 |
| 25 |
| 4 |
| 5 |
| 3 |
∴P2(
| 5 |
| 3 |
③如图3,当OA=AP,OM=PQ时,△OMP≌△PQO.
过O作OE⊥AB于点E,过P作PF⊥OA于点F.

∴△OEA≌△PFA.
PF=OE=-5.
把y=-5代入y=-
| 3 |
| 4 |
| 25 |
| 4 |
∴P3(15,-5).
综上所述,所有符合条件的点P的坐标为P1(5,
| 5 |
| 2 |
| 5 |
| 3 |
点评:本题考查了一次函数的综合题,利用了待定系数法求解析式,全等三角形的判定与性质,分类讨论是解题关键.

练习册系列答案
相关题目
将点(-5,4)向右平移5个单位、向下平移2个单位后的坐标为( )
| A、(-10,2) |
| B、(-10,0) |
| C、(0,-2) |
| D、(0,2) |
下列方程中,是二元一次方程的有( )
A、
| ||||
B、
| ||||
| C、y=-3x+3 | ||||
| D、mn+m=7 |
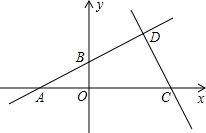 如图,在平面直角坐标系中,点O为坐标原点,A(-4,0),B(0,2),C(6,0),直线AB与直线CD相交于点D,D点横纵坐标相同.
如图,在平面直角坐标系中,点O为坐标原点,A(-4,0),B(0,2),C(6,0),直线AB与直线CD相交于点D,D点横纵坐标相同.