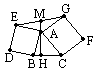
题目内容
| |||||||||||
答案:
解析:
解析:
(1) |
连结AO并延长与⊙O分别交于点C、D,则最短距离为AC的长 收切割线定理可求得 |
(2) |
CD与⊙O相切 证明:过点O作OE⊥CD于点E,连结OB 由题意知,四边形OBCE是矩形 又∵ ∴四边形OBCE是正方形 ∴OE=OB=3 故CD是⊙O的切线 |

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目