题目内容
两块完全一样的含30°角的三角板重叠在一起，若绕长直角边中点M转动，使上面一块的斜边刚好过下面一块的直角顶点，如图，∠A＝30°，AC＝10，则此时两直角顶点C、C′间的距离是_______．
【答案】
5.
【解析】
试题分析：连接C′C，
∵M是AC的中点，AC=10，△ABC，△A′B′C′是两块完全一样的含30°角三角板重叠在一起的，
∴AM=CM=
A′C′，即CM=A′M=C′M.∴△A′C′C为直角三角形.
∵CM=A′M，∴∠A′=∠A′CM=30°.
∵∠A′=∠A=30°，∴∠A′C′C=60°.
∴等腰三角形△MCC′是等边三角形.
∴C′C=CM=A′M=C′M=AC=5.
∴C′C长为5.
考点: 1.旋转的性质;2.等边三角形的判定与性质.
练习册系列答案
孟建平小学滚动测试系列答案
相关题目
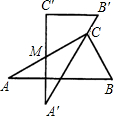角顶点，如图所示，∠A=30°，AC=10，则此时两直角顶点C，C′间的距离是
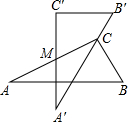（2011•太原二模）如图是两块完全一样的含30°角的直角三角板，将它们重叠在一起并绕其较长直角边的中点M转动，使上面一块三角板的斜边刚好过下面一块三角板的直角顶点C．已知AC=2，则这块直角三角板顶点A、A′之间的距离等于