题目内容
18.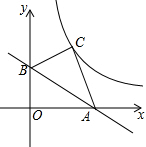 如图,在平面直角坐标系中,点A(2$\sqrt{3}$,0),点B(0,2),把△AOB沿直线AB翻折,点O落在了点C处,则图象过点C的反比例函数的解析式为( )
如图,在平面直角坐标系中,点A(2$\sqrt{3}$,0),点B(0,2),把△AOB沿直线AB翻折,点O落在了点C处,则图象过点C的反比例函数的解析式为( )| A. | y=$\frac{4}{x}$ | B. | y=$\frac{3\sqrt{3}}{x}$ | C. | y=$\frac{3-\sqrt{3}}{x}$ | D. | y=$\frac{-2\sqrt{3}}{x}$ |
分析 过点C作CD⊥OA,垂足为点D,利用三角函数即可求得C的坐标,然后利用待定系数法即可求得反比例函数的解析式.
解答 解:如图,过点C作CD⊥OA,垂足为点D,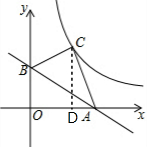
在Rt△AOB中,∠AOB=90°,
∴AB=$\sqrt{O{A}^{2}+O{B}^{2}}$=$\sqrt{(2\sqrt{3})^{2}+{2}^{2}}$=4,
∴AB=2BO,
∴∠BAO=30°,
∵△ABC由△AOB沿直线AB翻折所得,
∴∠CAB=∠BAO=30°,CA=AO=2$\sqrt{3}$.
∵CD⊥OA,垂足为点D,
∴∠CDA=90°,
∴∠ACD=90°-30°-30°=30°
∴AD=$\frac{1}{2}AC=\sqrt{3}$,
∴CD=$\sqrt{A{C}^{2}-A{D}^{2}}$=$\sqrt{(2\sqrt{3})^{2}-(\sqrt{3})^{2}}$=3,OD=OA-AD=$\sqrt{3}$,
∴C($\sqrt{3}$,3),
∵点C($\sqrt{3}$,3)在双曲线y=$\frac{k}{x}$上,
∴3=$\frac{k}{\sqrt{3}}$,解得:k=3$\sqrt{3}$,
∴反比例函数的解析式为y=$\frac{3\sqrt{3}}{x}$,
故选:B.
点评 本题考查了一次函数图象与几何变换以及待定系数法求函数的解析式,向坐标轴作垂线段,正确求得C的坐标是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.-$\frac{1}{8}$的立方根是( )
| A. | -$\frac{1}{2}$ | B. | $±\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | -$\frac{1}{4}$ |
10.15的负的平方根介于( )
| A. | -4与-3之间 | B. | -5与-4之间 | C. | -3与-2之间 | D. | -2与-1之间 |
 如图所示是从左面和从上面看由几个相同的小正方体组成的几何体得到的平面图形,则小正方体的个数最少是4.
如图所示是从左面和从上面看由几个相同的小正方体组成的几何体得到的平面图形,则小正方体的个数最少是4.
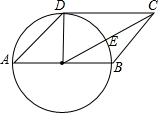 如图,在?ABCD中,AB=$\sqrt{2}$AD,以AB为直径的⊙O经过点D,连接OC交⊙O于点E.
如图,在?ABCD中,AB=$\sqrt{2}$AD,以AB为直径的⊙O经过点D,连接OC交⊙O于点E. 如图,把一个长方形纸条ABCD沿EF折叠,若∠1=55°,则∠AEG=70.
如图,把一个长方形纸条ABCD沿EF折叠,若∠1=55°,则∠AEG=70.