题目内容
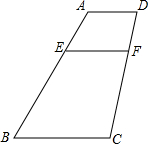 如图,梯形ABCD中,AD∥BC,E为线段AB上的点,且满足AE=AD,BE=BC,过E作EF∥BC交CD于F,设P为线段CD上任意一点,试说明
如图,梯形ABCD中,AD∥BC,E为线段AB上的点,且满足AE=AD,BE=BC,过E作EF∥BC交CD于F,设P为线段CD上任意一点,试说明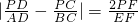 的理由.
的理由.
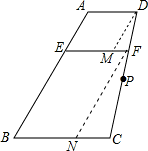 证明:如图,
证明:如图,过D、F分别作DM∥AB交EF于M,FN∥AB交BC于N,
得平行四边形ADME和平行四边形BEFN.
所以FM=EF-AD,CN=BC-EF,DM=AE=AD,FN=BE=BC.
由△DMF∽△FNC,得
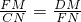 ,即
,即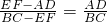 ,
,所以
 .
.又因为
 ,即
,即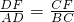 .
.所以当点P在线段CF上时,
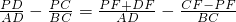
=
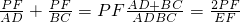 ,
,同理,当点P在线段DF上时,
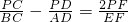 .所以
.所以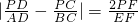 .
.分析:可过D、F分别作DM∥AB交EF于M,FN∥AB交BC于N,则可得平行四边形ADME和平行四边形BEFN以及△DMF∽△FNC,进而得出对应线段成比例,再通过线段之间的转化,即可得出结论.
点评:本题主要考查了梯形的性质以及相似三角形的判定及性质,能够利用其性质求解一些计算、证明问题.

练习册系列答案
相关题目
 已知,如图,梯形ABCD中,AD∥BC,∠B=45°,∠C=120°,AB=8,则CD的长为( )
已知,如图,梯形ABCD中,AD∥BC,∠B=45°,∠C=120°,AB=8,则CD的长为( )A、
| ||||
B、4
| ||||
C、
| ||||
D、4
|
 5、已知:如图,梯形ABCD中,AD∥BC,AB=DC,AC、BD相交于点O,那么,图中全等三角形共有
5、已知:如图,梯形ABCD中,AD∥BC,AB=DC,AC、BD相交于点O,那么,图中全等三角形共有 10、如图,梯形ABCD中,AD∥BC,BD为对角线,中位线EF交BD于O点,若FO-EO=3,则BC-AD等于( )
10、如图,梯形ABCD中,AD∥BC,BD为对角线,中位线EF交BD于O点,若FO-EO=3,则BC-AD等于( ) 如图,梯形ABCD中,已知AD∥BC,∠A=90°,AB=7,AD=2,
如图,梯形ABCD中,已知AD∥BC,∠A=90°,AB=7,AD=2, 如图,梯形ABCD中,AD∥BC,BC=5,AD=3,对角线AC⊥BD,且∠DBC=30°,求梯形ABCD的高.
如图,梯形ABCD中,AD∥BC,BC=5,AD=3,对角线AC⊥BD,且∠DBC=30°,求梯形ABCD的高.