题目内容
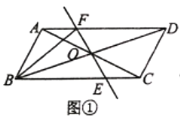
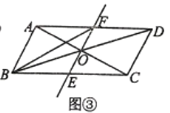
【题目】已知:如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() .点
.点![]() 从点
从点![]() 开始沿
开始沿![]() 边向点
边向点![]() 以
以![]() 的速度移动,同时点
的速度移动,同时点![]() 从点
从点![]() 开始沿
开始沿![]() 边向点
边向点![]() 以
以![]() 的速度移动.当一个点到达终点时另一点也随之停止运动,设运动时间为
的速度移动.当一个点到达终点时另一点也随之停止运动,设运动时间为![]() 秒,
秒,

![]() 求几秒后,
求几秒后,![]() 的面积等于
的面积等于![]() ?
?
![]() 求几秒后,
求几秒后,![]() 的长度等于
的长度等于![]() ?
?
![]() 运动过程中,
运动过程中,![]() 的面积能否等于
的面积能否等于![]() ?说明理由.
?说明理由.
【答案】(1)![]() 或
或![]() 秒后
秒后![]() 的面积等于
的面积等于![]() ;(2)当
;(2)当![]() 或
或![]() 时,
时,![]() 的长度等于
的长度等于![]() ;(3)
;(3)![]() 的面积不能等于
的面积不能等于![]() .
.
【解析】
(1)设经过x秒钟,△PBQ的面积等于6平方厘米,根据点P从A点开始沿AB边向点B以1cm/s的速度移动,点Q从B点开始沿BC边向点C以2cm/s的速度移动,表示出BP和BQ的长可列方程求解.
(2)根据PQ=5,利用勾股定理BP2+BQ2=PQ2,求出即可;
(3)通过判定得到的方程的根的判别式即可判定能否达到8cm2.
(1)设经过x秒以后△PBQ面积为6
![]() ×(5x)×2x=6
×(5x)×2x=6
整理得:x25x+6=0
解得:x=2或x=3
答:2或3秒后△PBQ的面积等于6cm2.
![]() 当
当![]() 时,在
时,在![]() 中,∵
中,∵![]() ,
,
∴![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
∴当![]() 或
或![]() 时,
时,![]() 的长度等于
的长度等于![]() .
.
![]() 设经过
设经过![]() 秒以后
秒以后![]() 面积为
面积为![]() ,
,
![]()
整理得:![]()
![]()
∴![]() 的面积不能等于
的面积不能等于![]() .
.

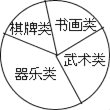
【题目】某校学生会准备调查六年级学生参加“武术类”、“书画类”、“棋牌类”、“器乐类”四类校本课程的人数.
(1)确定调查方式时,甲同学说:“我到六年级(1)班去调查全体同学”;乙同学说:“放学时我到校门口随机调查部分同学”;丙同学说:“我到六年级每个班随机调查一定数量的同学”.请指出哪位同学的调查方式最合理.
类别 | 频数(人数) | 频率 |
武术类 | 0.25 | |
书画类 | 20 | 0.20 |
棋牌类 | 15 | b |
器乐类 | ||
合计 | a | 1.00 |
(2)他们采用了最为合理的调查方法收集数据,并绘制了如图所示的统计表和扇形统计图.
请你根据以上图表提供的信息解答下列问题:
①a=_____,b=_____;
②在扇形统计图中,器乐类所对应扇形的圆心角的度数是_____;
③若该校六年级有学生560人,请你估计大约有多少学生参加武术类校本课程.