Question

【题目】已知为坐标原点，点是反比例函数上的点，过点作直线，直线交轴的正半轴于点，点的坐标为．设三角形的面积为，且．

（1）当时，求点的坐标；

（2）若，求反比例函数的解析式；

（3）在（2）的结论下，设反比例函数上的一动点，是小于20的整数，求的最小值．

Answer 1

【答案】（1）点的坐标为；（2）；（3）的最小值为5

【解析】

（1）根据三角形的面积公式得到S=，而，把代入就可以得到a的值；

（2）易证△OQA是等腰直角三角形，得到，根据三角形的面积S=，就可以解得k的值;

（3）由勾股定理易得，而当，最小，结合是整数即可求得结果．

解：（1）过点作于，则

当时，，所以，

即点的坐标为．

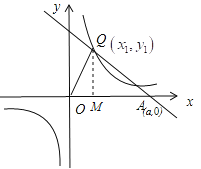
（2）因为，，所以三角形是等腰直角三角形．

所以，

即

又点是反比例函数上的点，则

所以，反比例函数的解析式为．

（3）因为

所以当，即当时，最小；

又因为是整数，而当时，；当时，．

所以的最小值为5．