题目内容
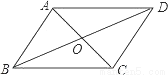
1. 如图,△ABC中,∠ABC=52°,∠BAD=12°,DC=AB,则∠CAD=64°.
如图,△ABC中,∠ABC=52°,∠BAD=12°,DC=AB,则∠CAD=64°.
分析 在CD上取点E,使得BE=AB=CD,由AB=BE,利用等角对等边得到一对角相等,由顶角∠B的度数,求出底角∠BAE的度数,利用三角形的外角性质由∠B+∠BAD求出∠ADE的度数,在三角形ADC中,由∠C与∠ADE的度数,利用三角形的内角和定理即可求出∠CAD的度数.
解答  解:在CD上取点E,使得BE=AB,由AB=CD,得到BE=AB=CD,
解:在CD上取点E,使得BE=AB,由AB=CD,得到BE=AB=CD,
∵BA=BE,且∠ABC=52°,
∴∠BAE=∠BEA=64°,
又∵∠BAD=12°,
∴∠ADE=∠B+∠BAD=64°,
∴∠ADE=∠AED,
∴AD=AE,
又∵BE=CD,
∴BE-DE=CD-DE,即BD=EC,
∵∠ADB=∠AEC=116°,
∴△ABD≌△ACE(SAS),
∴∠B=∠C=52°,
在ADC中,∠ADE=64°,∠C=52°,
∴∠CAD=64°.
故答案为:64°.
点评 此题考查了等腰三角形的性质,三角形的外角性质,以及三角形的内角和定理,熟练掌握性质及定理是解本题的关键.

练习册系列答案
相关题目
13.随着天气变热,很多学生都想去游泳,但是野外游泳非常危险,并且很不卫生,我国每年大约有5万青少年或儿童死于溺水,在非正常死亡中占较大比例,因此,我们一定不要私自在野外游泳,最理想的地方是游泳馆.有一家游泳馆的收费为30元/次,若购买会员年卡,可享受如下优惠:
例如,购买A类会员年卡,一年内游泳20次,消费50+25×20=550元,若一年内在该游泳馆游泳的次数介于45~55次之间,则最省钱的方式为( )
| 会员年卡类型 | 办卡费用(元) | 每次游泳收费(元) |
| A 类 | 50 | 25 |
| B 类 | 200 | 20 |
| C 类 | 400 | 15 |
| A. | 购买A类会员年卡 | B. | 购买B类会员年卡 | C. | 购买C类会员年卡 | D. | 不购买会员年卡 |


 B. tanA=
B. tanA= C. cosB=
C. cosB= D. tanB=
D. tanB=
 中,
中,  ,
,  、
、 、
、 分别为
分别为 、
、 、
、 的中点,已知
的中点,已知 ,则
,则 ________.
________.

 如图.在△ABC中,△ABC的高AD、CE相交于点H,∠B=57°,则∠AHC=123°度.
如图.在△ABC中,△ABC的高AD、CE相交于点H,∠B=57°,则∠AHC=123°度.