题目内容
已知点P为⊙O内一点,且OP=4,⊙O的半径为5.若过P的弦AB的长度为整数,则弦AB的值可以有( )
分析:EF为过P点的直径,CD⊥EF于P,连结OD,根据垂径定理得到PD=PC,再利用勾股定理计算出PD=3,则CD=6,由于过P点最长的弦EF=10,最短的弦CD=6,
所以过P的弦AB的长度为整数,则弦AB的值可以6,7,8,9,10.
所以过P的弦AB的长度为整数,则弦AB的值可以6,7,8,9,10.
解答: 解:如图,EF为过P点的直径,CD⊥EF于P,连结OD,
解:如图,EF为过P点的直径,CD⊥EF于P,连结OD,
∴PD=PC,
在Rt△ODP中,OP=4,OD=5,
∴PD=
=3,
∴CD=6,
∵过P点最长的弦EF=10,最短的弦CD=6,
∴若过P的弦AB的长度为整数,则弦AB的值可以6,7,8,9,10.
故选B.
 解:如图,EF为过P点的直径,CD⊥EF于P,连结OD,
解:如图,EF为过P点的直径,CD⊥EF于P,连结OD,∴PD=PC,
在Rt△ODP中,OP=4,OD=5,
∴PD=
| 52-42 |
∴CD=6,
∵过P点最长的弦EF=10,最短的弦CD=6,
∴若过P的弦AB的长度为整数,则弦AB的值可以6,7,8,9,10.
故选B.
点评:本题考查了垂径定理:平分弦的直径平分这条弦,并且平分弦所对的两条弧;推论:平分弦所对一条弧的直径,垂直平分弦,并且平分弦所对的另一条弧也考查了勾股定理.

练习册系列答案
相关题目
 如图,已知点A为⊙O内一点,点B、C均在圆上,∠A=∠B=45°,∠C=30°,线段OA=
如图,已知点A为⊙O内一点,点B、C均在圆上,∠A=∠B=45°,∠C=30°,线段OA= 如图,已知点A为⊙O内一点,点B、C均在圆上,∠A=∠B=45°,∠C=30°,线段OA=
如图,已知点A为⊙O内一点,点B、C均在圆上,∠A=∠B=45°,∠C=30°,线段OA= -1.求阴影部分的面积(结果保留π)
-1.求阴影部分的面积(结果保留π)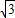 -1.求阴影部分的面积(结果保留π)
-1.求阴影部分的面积(结果保留π)