题目内容
 如图,已知点A为⊙O内一点,点B、C均在圆上,∠A=∠B=45°,∠C=30°,线段OA=
如图,已知点A为⊙O内一点,点B、C均在圆上,∠A=∠B=45°,∠C=30°,线段OA=| 3 |
分析:延长AO交BC于点D,连接OB,由∠A=∠ABC=45°,得到AD=BD,∠ADB=90°,即AD⊥BC.根据垂径定理得到BD=CD.在Rt△COD中,设OD=x,∠C=30°,得到OC=2x,CD=
x=AD,则OA=AD-OD=
x-x=(
-1)x=
-1,解得x=1,则OD=1,OC=2,BC=2CD=2
,分别利用三角形和扇形的面积公式计算S扇形OBC,和S△COB,然后利用S阴影=S扇形OBC-S△COB计算即可.
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
解答: 解:延长AO交BC于点D,连接OB.
解:延长AO交BC于点D,连接OB.
∵∠A=∠ABC=45°,
∴AD=BD,∠ADB=90°,即AD⊥BC.
∴BD=CD.
在Rt△COD中,设OD=x,
∵∠C=30°,
∴∠COD=60°,OC=2x,CD=
x.
∴∠COB=120°,AD=
x.
∴OA=AD-OD=
x-x=(
-1)x.
而OA=
-1,
∴x=1,即OD=1,OC=2,BC=2CD=2
.
∴S阴影=S扇形OBC-S△COB=
π×22-
×2
×1=
π-
.
 解:延长AO交BC于点D,连接OB.
解:延长AO交BC于点D,连接OB.∵∠A=∠ABC=45°,
∴AD=BD,∠ADB=90°,即AD⊥BC.
∴BD=CD.
在Rt△COD中,设OD=x,
∵∠C=30°,
∴∠COD=60°,OC=2x,CD=
| 3 |
∴∠COB=120°,AD=
| 3 |
∴OA=AD-OD=
| 3 |
| 3 |
而OA=
| 3 |
∴x=1,即OD=1,OC=2,BC=2CD=2
| 3 |
∴S阴影=S扇形OBC-S△COB=
| 120 |
| 360 |
| 1 |
| 2 |
| 3 |
| 4 |
| 3 |
| 3 |
点评:本题考查了扇形的面积公式:S=
(n为圆心角的度数,R为圆的半径).也考查了含30度得直角三角形三边的关系和三角形的面积公式.
| n•πR2 |
| 360 |

练习册系列答案
相关题目
 如图,已知点C为线段AE上一点,AE=8cm,△ABC和△CDE为AE同侧的两个等边三角形,连接BE交CD于N,连接AD交BC于M,连接MN.
如图,已知点C为线段AE上一点,AE=8cm,△ABC和△CDE为AE同侧的两个等边三角形,连接BE交CD于N,连接AD交BC于M,连接MN. (2012•龙湖区模拟)如图,已知点P为反比例函数
(2012•龙湖区模拟)如图,已知点P为反比例函数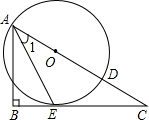 (2012•玉林)如图,已知点O为Rt△ABC斜边AC上一点,以点O为圆心,OA长为半径的⊙O与BC相切于点E,与AC相交于点D,连接AE.
(2012•玉林)如图,已知点O为Rt△ABC斜边AC上一点,以点O为圆心,OA长为半径的⊙O与BC相切于点E,与AC相交于点D,连接AE. 如图,已知点D为△ABC中AC边上一点,且AD:DC=3;4,设
如图,已知点D为△ABC中AC边上一点,且AD:DC=3;4,设 如图,已知点D为等腰直角△ABC内一点,AC=BC,∠CAD=∠CBD=15°,E为AD延长线上的一点,且CE=CA.若DE=acm,BD=bcm(a>b),则CD=
如图,已知点D为等腰直角△ABC内一点,AC=BC,∠CAD=∠CBD=15°,E为AD延长线上的一点,且CE=CA.若DE=acm,BD=bcm(a>b),则CD=