题目内容
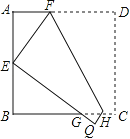
【题目】(![]() 分)在菱形
分)在菱形![]() 中,
中, ![]() ,
, ![]() ,点
,点![]() 是线段
是线段![]() 上的一个动点.
上的一个动点.
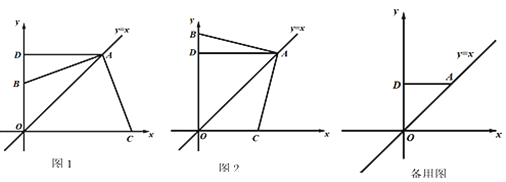
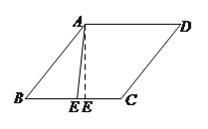
(![]() )如图①,求
)如图①,求![]() 的最小值.
的最小值.
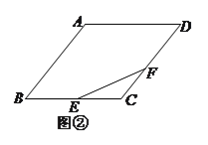
(![]() )如图②,若
)如图②,若![]() 也是
也是![]() 边上的一个动点,且
边上的一个动点,且![]() ,求
,求![]() 的最小值.
的最小值.
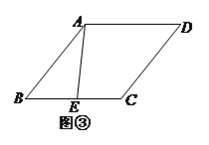
(![]() )如图③,若
)如图③,若![]() ,则在菱形内部存在一点
,则在菱形内部存在一点![]() ,使得点
,使得点![]() 分别到点
分别到点![]() 、点
、点![]() 、边
、边![]() 的距离之和最小.请你画出这样的点
的距离之和最小.请你画出这样的点![]() ,并求出这个最小值.
,并求出这个最小值.

【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】试题分析:(1)根据正弦的定义求出AE的最小值;
(2)连接![]() 、
、![]() 、
、![]() ,在菱形
,在菱形![]() 中,可证
中,可证![]() 为等边三角形,
为等边三角形,
![]() 的最小值即为
的最小值即为![]() 的最小值
的最小值![]() .
.
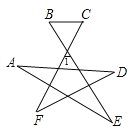
(3)以![]() 为边在菱形外作等边
为边在菱形外作等边![]() ,作
,作![]() 于
于![]() ,
, ![]() 即为点
即为点![]() 分别到点
分别到点![]() 、点
、点![]() 、边
、边![]() 的距离之和最小,当
的距离之和最小,当![]() 于
于![]() 时,点
时,点![]() 即为所求.
即为所求.
试题解析:(![]() )根据垂线段最短,当
)根据垂线段最短,当![]() 时,
时, ![]() 最小,最小为菱形的高
最小,最小为菱形的高![]() .
.
(![]() )连接
)连接![]() 、
、![]() 、
、![]() ,
,
在菱形![]() 中,可证
中,可证![]() 为等边三角形,
为等边三角形,
![]() 的最小值即为
的最小值即为![]() 的最小值
的最小值![]() .
.
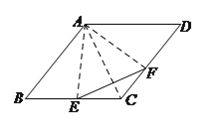
(![]() )如图,以
)如图,以![]() 为边在菱形外作等边
为边在菱形外作等边![]() ,
,
作![]() 于
于![]() ,
, ![]() 即为点
即为点![]() 分别到点
分别到点![]() 、点
、点![]() 、边
、边![]() 的距离之和最小,
的距离之和最小,
当![]() 于
于![]() 时,点
时,点![]() 即为所求.理由如下:
即为所求.理由如下:
当![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到
得到![]() ,点
,点![]() 在
在![]() 上,
上,
此时![]() ,
, ![]() ,
, ![]() ,
,
要使点![]() 分别到点
分别到点![]() 、点
、点![]() 、边
、边![]() 的距离之和最小,
的距离之和最小,
则要![]() 即可.
即可.
作![]() ,
,
由题意可得: ![]() 为
为![]() 的中点.
的中点.
在![]() 中,
中, ![]() ,
, ![]() ,
,
∴![]() ,
, ![]() ,
,
∴![]() .
.


练习册系列答案
相关题目