题目内容
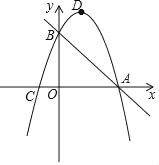
【题目】(![]() 分)如图,抛物线
分)如图,抛物线![]() 的顶点为
的顶点为![]() .
.
(![]() )求抛物线
)求抛物线![]() 的函数表达式.
的函数表达式.
(![]() )若抛物线形
)若抛物线形![]() 与
与![]() 关于
关于![]() 轴对称,求抛物线
轴对称,求抛物线![]() 的函数表达式.
的函数表达式.
(![]() )在(
)在(![]() )的基础上,设
)的基础上,设![]() 上的点
上的点![]() 、
、![]() 始终与
始终与![]() 上的点
上的点![]() 、
、![]() 分别关于
分别关于![]() 轴对称,是否存在点
轴对称,是否存在点![]() 、
、![]() (
(![]() 、
、![]() 分别位于抛物线对称轴两侧,且
分别位于抛物线对称轴两侧,且![]() 在
在![]() 的左侧),使四边形
的左侧),使四边形![]() 为正方形?
为正方形?
若存在,求出点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
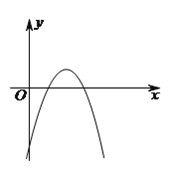
【答案】(1)y=-x2+6x-7;(2)y=x2-6x+7;(3)存在,(2,1)或(1,-2)
【解析】试题分析: ![]() 根据顶点坐标,求出
根据顶点坐标,求出![]() 的值,求抛物线
的值,求抛物线![]() 的函数表达式.
的函数表达式.
![]() 抛物线
抛物线![]() 与
与![]() 关于
关于![]() 轴对称,求出抛物线
轴对称,求出抛物线![]() 的顶点坐标和二次项系数,即可求得函数表达式.
的顶点坐标和二次项系数,即可求得函数表达式.
![]() 根据正方形的边长相等,
根据正方形的边长相等, ![]() .列出方程,求解即可.
.列出方程,求解即可.
试题解析:
(![]() )抛物线
)抛物线![]() 的顶点为
的顶点为![]() .
.
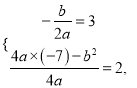
解得: ![]()
![]() .
.
(![]() )若抛物线
)若抛物线![]() 的顶点坐标为
的顶点坐标为![]() .
. ![]()
若抛物线![]() 与
与![]() 关于
关于![]() 轴对称,
轴对称,
抛物线![]() 的顶点坐标为:
的顶点坐标为: ![]()
![]()
抛物线![]() 的函数表达式为:
的函数表达式为:
![]() .
.
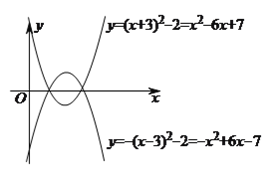
(![]() )存在.
)存在.
如图,要使四边形![]() 是正方形,
是正方形,
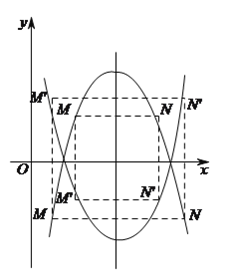
∵![]() 轴,则要
轴,则要![]() 轴,
轴,
且![]() .
.
设![]() ,
, ![]() ,
,
∵抛物线的对称轴为:直线![]() ,
,
∴由抛物线的对称性可知![]() ,
,
∴![]() .
.
当![]() ,
,
解得: ![]() ,(
,( ![]() 舍去),此时
舍去),此时![]() ,
,
当![]() 时,
时, ![]() ,
,
解得: ![]() ,(
,( ![]() 舍去),此时
舍去),此时![]() ,
,
综上,存在这样的点![]() 或
或![]() .
.

练习册系列答案
相关题目